|
|
|
|
|
Глава 8. Функция у = х2 § 37. Функция у = х2 и её графикВ главе 2 мы ввели термин «линейная функция», понимая под этим линейное уравнение вида у = kx + m с двумя переменными х, у. Правда, переменные х, у, фигурирующие в этом уравнении (в этой математической модели), считались неравноправными: х — независимая переменная (аргумент), которой мы могли придавать любые значения, независимо ни от чего; у — зависимая переменная, поскольку её значение зависело от того, какое значение переменной х было выбрано.
Но тогда возникает естественный вопрос: а не встречаются ли математические модели такого же плана, но такие, у которых у выражается через х не по формуле у = kx + m, а каким-то иным способом? Ответ ясен: конечно, встречаются. Если, например, х — сторона квадрата, а у — его площадь, то у = х2. Если х — сторона куба, а у — его объём, то у = х3. Если х — одна сторона прямоугольника, площадь которого равна 100 см2, а у — другая его сторона, то Замечание. Выше мы уже не раз говорили о том, как обстоит дело в математике с новыми понятиями, новыми терминами. Часто бывает так: ввели новое понятие, работают с ним, но затем, по мере дальнейшего изучения математики, начинают осознавать, что введённое понятие требует уточнения, развития. Именно так обстояло дело с понятием «тождество». Точно так же обстоит дело и с понятием «функция». Мы ещё довольно долго будем привыкать к нему, набираться опыта, работать с этим понятием, пока не придём к строгому определению (это будет в 9-м классе). В этом параграфе мы рассмотрим функцию у = х2 и построим её график. Дадим независимой переменной х несколько конкретных значений и вычислим соответствующие значения зависимой переменной у (по формуле у = х2): если х = 0, то у = 02 = 0;
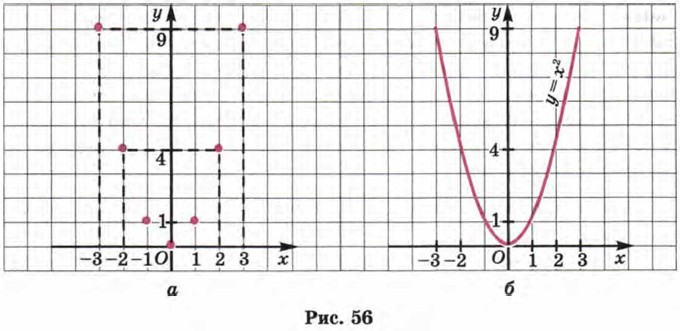
Короче говоря, мы составили следующую таблицу:
Построим найденные точки (0; 0), (1; 1), (2; 4), (3; 9), (-1; 1), (-2; 4), (-3; 9) на координатной плоскости хОу (рис. 56, а). Эти точки расположены на некоторой линии, начертим её (рис. 56,б). Эту линию называют параболой.
Конечно, в идеале надо было дать аргументу х все возможные значения, вычислить соответствующие значения переменной у и построить полученные точки (х; у). Тогда график был бы абсолютно точным, безупречным. Однако это нереально, ведь таких точек бесконечно много. Поэтому математики поступают так: берут конечное множество точек, строят их на координатной плоскости и смотрят, какая линия намечается этими точками. Если контуры этой линии проявляются достаточно отчётливо (как это было у нас, скажем, в примере 1 из § 7, см. с. 40), то эту линию проводят. Возможны ли ошибки? Не без этого. Поэтому и надо всё глубже и глубже изучать математику, чтобы были возможности избегать ошибок.
|
|
|




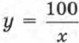 . Поэтому, естественно, приходится изучать и модель у = х2, и модель у = х , и модель
. Поэтому, естественно, приходится изучать и модель у = х2, и модель у = х , и модель