Главная >> Алгебра 7 класс Мордкович

Глава 8. Функция у = х²

§ 37. Функция у = х² и её график (продолжение)

Попробуем, глядя на рисунок 56,б, описать геометрические свойства параболы.

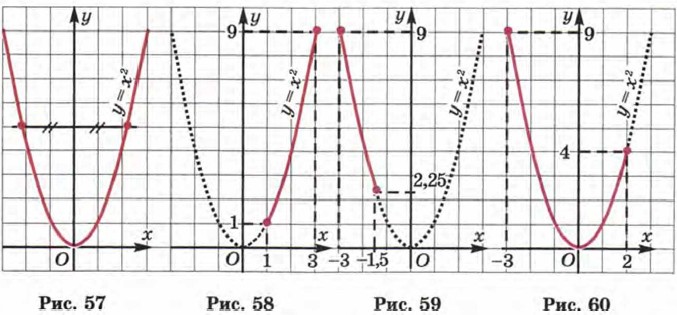
Во-первых, отмечаем, что парабола обладает симметрией. В самом деле, если провести выше оси х любую прямую, параллельную оси х, то эта прямая пересечёт параболу в двух точках, расположенных на равных расстояниях от оси у, но по разные стороны от неё (рис. 57). Кстати, то же можно сказать и о точках, отмеченных на рисунке 56, а: (1; 1) и (-1; 1); (2; 4) и (-2; 4); (3; 9) и (-3; 9). Говорят, что ось у является осью симметрии параболы у = х² или что парабола симметрична относительно оси у.

Во-вторых, замечаем, что ось симметрии как бы разрезает параболу на две части, которые обычно называют ветвями параболы.

В-третьих, отмечаем, что у параболы есть особая точка, в которой смыкаются обе ветви и которая лежит на оси симметрии параболы — точка (0; 0). Учитывая её особенность, ей присвоили специальное название — вершина параболы.

В-четвёртых, когда одна ветвь параболы соединяется в вершине с другой ветвью, это происходит плавно, без излома; парабола как бы «прижимается» к оси абсцисс. Обычно говорят: парабола касается оси абсцисс.

Теперь попробуем, глядя на рисунок 56,б, описать некоторые свойства функции у = х².

Во-первых, замечаем, что у = 0 при х = 0, у > 0 при х > 0 и при х < 0.

Во-вторых, отмечаем, что y_наим = 0, а у_наи6 не существует.

В-третьих, замечаем, что функция у = х² убывает на луче (-∞; 0] — при этих значениях х, двигаясь по параболе слева направо, мы «спускаемся с горки». Функция у = х² возрастает на луче [0; +∞) — при этих значениях х, двигаясь по параболе слева направо, мы «поднимаемся в горку».

Пример 1. Найти наибольшее и наименьшее значения функции у = х²:

а) на отрезке [1; 3];
б) на отрезке [-3; —1,5];
в) на отрезке [-3; 2].

Р е ш е н и е.

а) Построим параболу у = х² и выделим ту её часть, которая соответствует значениям переменной х из отрезка [1; 3] (рис. 58). Для выделенной части графика находим y_наим = 1 (при х = 1), y_наи6 = 9 (при х = 3).

б) Построим параболу у = х² и выделим ту её часть, которая соответствует значениям переменной х из отрезка [-3; -1,5] (рис. 59). Для выделенной части графика находим y_наим = 2,25 (при х = -1,5), y_наиб = 9 (при x = -3).

в) Построим параболу у = х² и выделим ту её часть, которая соответствует значениям переменной х из отрезка [-3; 2] (рис. 60). Для выделенной части графика находим y_нанм = 0 (при х = 0), y_наиб = 9 (при x = -3).

С о в е т. Чтобы каждый раз не строить график функции у = х² по точкам, вырежьте из плотной бумаги шаблон параболы. С его помощью вы будете очень быстро чертить параболу.

Замечание. Предлагая вам заготовить шаблон параболы, мы как бы уравниваем в правах функцию у = х² и линейную функцию у = kх + m. Ведь графиком линейной функции является прямая, а для изображения прямой используется обычная линейка — это и есть шаблон графика функции у = kх + m. Так пусть у вас будет и шаблон графика функции у = х².

<<< К началу      Окончание >>>