|
|
|
|
|
Глава 8. Функция у = х2 § 39. Что означает в математике запись у = ƒ(x) (окончание)
Обсудим одно из таких новых свойств. График функции, рассмотренной в примере 4, состоит из трёх ветвей (из трёх «кусочков»). Первая и вторая ветви (отрезок прямой у = х + 2 и часть параболы) «состыкованы» удачно: отрезок заканчивается в точке (-1; 1), а участок параболы начинается в той же точке. А вот вторая и третья ветви менее удачно «состыкованы»: третья ветвь («кусочек» горизонтальной прямой) начинается не в точке (0; 0), а в точке (0; 4). Математики говорят так: «функция у = ƒ(x) претерпевает разрыв при х = 0 (или в точке х = 0)». Если функция не имеет точек разрыва, то её называют непрерывной. Так, все функции, с которыми мы познакомились в предыдущих параграфах (у = b, у = kx, у = kx + m, у = х2, у = -х2), — непрерывные. Пример 5. Дана функция Р е ш е н и е. Как видите, здесь функция задана достаточно сложным выражением. Но математика — единая и цельная наука, её разделы тесно связаны друг с другом. Воспользуемся тем, что мы изучали в главе 7, и сократим алгебраическую дробь
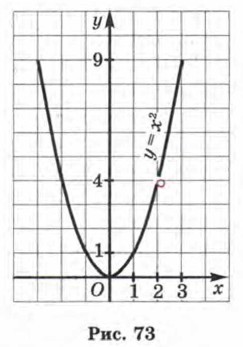
Итак, на самом деле ƒ(x) = x2. Правда, надо учесть, что тождество Построим на координатной плоскости хОу параболу у = х2. Прямая х = 2 пересекает её в точке (2; 4). Но по условию х ≠ 2, значит, точку (2; 4) параболы мы должны исключить из рассмотрения, для чего на чертеже отметим эту точку светлым кружком. Таким образом, график функции построен — это парабола у = х2 с «выколотой» точкой (2; 4) (рис. 73).
Перейдём к описанию свойств функции у = ƒ(x), т. е. к чтению её графика. 1. Независимая переменная х принимает любые значения, кроме х = 2. Значит, область определения функции состоит из двух открытых лучей (-∞; 2) и (2; +∞). 2. унаим = 0 (достигается при х = 0), yнаи6 не существует. 3. Функция претерпевает разрыв при х = 2 (в точке х = 2); на (-∞; 2) и на (2; +∞) она непрерывна. 4. у = 0, если х = 0. 5. у > 0, если х е (-∞; 0), если х ∈ (0; 2) и если x ∈ (2; +∞). 6. Функция убывает на луче (-∞; 0], возрастает на полуинтервале [0; 2) и на открытом луче (2; +∞). Вопросы для самопроверки 1. Известно, что ƒ(x) = 2х + 3. Найдите: a)ƒ(2x); б) ƒ(2x + 3). 2. Известно, что ƒ(x) = х2. Найдите: а) ƒ(2х); б) ƒ(2x + 3); в) ƒ(-x); г) ƒ(x6). 3. Известно, что ƒ(x) = -х2. Найдите: a) ƒ(0,5x); б) ƒ(x - 3); в) ƒ(-2x); г) ƒ(-x3). 4. Как вы понимаете, что такое кусочная функция? 5. Приведите пример кусочной функции у = ƒ(x), в котором задание вычислить ƒ(17) является некорректным. 6. Придумайте кусочную функцию, график которой состоит из части параболы и луча графика линейной функции. Задайте её аналитически (с помощью формул). 7. Придумайте кусочную функцию, график которой состоит из части параболы и двух отрезков графиков разных линейных функций. Задайте её аналитически. 8. Приведите пример функции, которая претерпевает разрыв при х = 1. 9. Сколько свойств функции мы уже можем записать, когда выполняем чтение графика? Перечислите эти свойства.
|
|
|




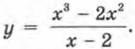 Построить и прочитать её график.
Построить и прочитать её график.
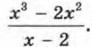 Имеем
Имеем
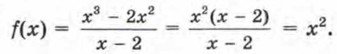
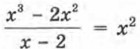 справедливо лишь при ограничении х ≠ 2. Следовательно, мы можем переформулировать задачу так: вместо функции
справедливо лишь при ограничении х ≠ 2. Следовательно, мы можем переформулировать задачу так: вместо функции 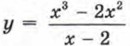 будем рассматривать функцию у = х2, где х ≠ 2.
будем рассматривать функцию у = х2, где х ≠ 2.