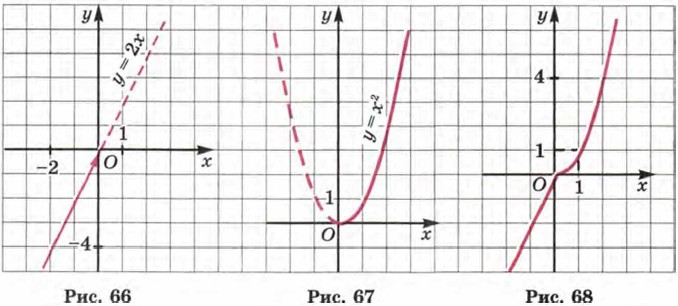
§ 39. Что означает в математике запись у = ƒ(x) (продолжение)

Вычислим ƒ(1,5), т. е. значение функции у = ƒ(x) в точке х = 1,5. Это значение х удовлетворяет условию х ≥ 0, и, следовательно, функция задаётся выражением, стоящим во второй строке, т. е. ƒ(x) = х2. Поэтому ƒ(1,5) = 1,52 = 2,25.

Аналогично находим ƒ(4): если х = 4, то х ≥ 0 и, значит, ƒ(x) = х², т. е. ƒ(4) = 4² = 16.

Осталось вычислить ƒ(0). Значение х = 0 удовлетворяет условию х ≥ 0, следовательно, ƒ(x) = х², т. е. ƒ(0) = 0² = 0.

б) Мы умеем строить графики функций у = 2х (рис. 66) и у = х² (рис. 67). Заданная функция у = ƒ(x) совпадает с функцией у = 2х при х < 0 — эта часть графика выделена на рисунке 66. Заданная функция у = ƒ(x) совпадает с функцией у = х² при х ≥ 0 — эта часть графика выделена на рисунке 67. Если мы теперь изобразим обе выделенные части в одной системе координат, то получим требуемый график функции у = ƒ(x) (рис. 68).

Конечно, математики не строят подобные графики так долго. Обычно всё делается сразу в одной системе координат. Только, естественно, прямая у = 2х берётся не целиком, а лишь при условии х < 0, т. е. на промежутке (-∞; 0), и парабола у = х² берётся не целиком, а лишь при условии х ≥ 0, т. е. на промежутке [0; +∞). Вот так «по кусочкам» и воспроизводится весь график. Поэтому функции такого типа, как в примере 3, называют кусочными функциями.

Пример 4. Дана функция у = ƒ(x), где

а) Вычислить: ƒ(-4), ƒ(-2), ƒ(-0,5), ƒ(0), ƒ(1), ƒ(5);

б) построить график функции у = ƒ(x).

Р е ш е н и е.

а) Значение х = -4 удовлетворяет условию -4 ≤ х ≤ -1, а в этом случае ƒ(x) = х + 2. Поэтому ƒ(-4) = -4 + 2 = -2.

Значение х = -2 удовлетворяет условию -4 ≤ х ≤ -1,ав этом случае ƒ(x) = х + 2. Значит, ƒ(-2) = -2 + 2 = 0.

Значение х = -0,5 удовлетворяет условию -1 < х ≤ 0, а в этом случае ƒ(x) = х². Следовательно, ƒ(-0,5) = (-0,5)² = 0,25.

Значение х = 0 удовлетворяет условию -1 < х ≤ 0, ав этом случае ƒ(x) = х². Тогда ƒ(0) = 0² = 0.

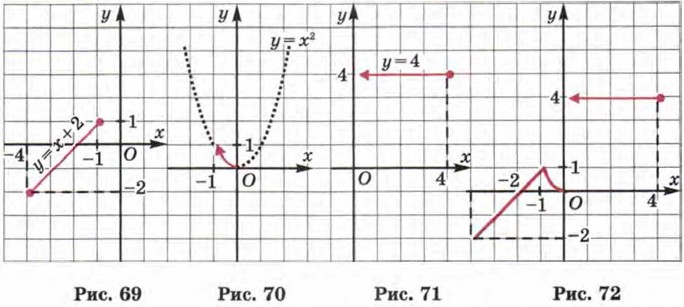
Значение х = 1 удовлетворяет условию 0 < х ≤ 4, а в этом случае ƒ(x) = 4; в частности, и ƒ(1) = 4.

Значение х = 5 не удовлетворяет ни одному из имеющихся условий: ни первому -4 ≤ х ≤ -1, ни второму -1 < х ≤ 0, ни третьему 0 < х ≤ 4. Поэтому вычислить ƒ(5) мы не можем, это задание некорректно.

б) График функции у = ƒ(x) построим «по кусочкам». На рисунке 69 изображён график функции у = х + 2, где х ∈ [-4; -1]. На рисунке 70 представлен график функции у = х², где х ∈ (-1; 0]. На рисунке 71 изображён график функции у = 4, где х ∈ (0; 4]. Наконец, на рисунке 72 все «кусочки» воссоединены в одно целое — в график функции у = ƒ(x).

Вот так с помощью известных графиков «по кусочкам» можно строить графики на координатной плоскости.

Опишем с помощью построенного на рисунке 72 графика некоторые свойства функции у = ƒ(x) — такое описание свойств обычно называют чтением графика. Чтение графика — это своеобразный переход от геометрической модели (от графической модели) к словесной модели (к описанию свойств функции). А построение графика — это переход от аналитической модели (она представлена в условии примера 4) к геометрической модели.

Итак, приступаем к чтению графика функции у = ƒ(x) (см. рис. 72).

1. Независимая переменная х «пробегает» все значения от -4 до 4. Иными словами, для каждого значения х из отрезка [-4; 4] можно вычислить значение функции ƒ(x). Говорят так: [-4; 4] — область определения функции.

Почему при решении примера 4 мы сказали, что найти ƒ(5) нельзя? Да потому, что значение х = 5 не принадлежит области определения функции.

2. у_наим = -2 (этого значения функция достигает при х = -4); y_наиб = 4 (этого значения функция достигает в любой точке полуинтервала (0; 4]).

3. у = 0, если х = -2 и если х = 0; эти точки графика функции у = ƒ(x) принадлежат оси х.

4. у > 0, если х ∈ (-2; 0) или если х ∈ (0; 4]; на этих промежутках график функции у = ƒ(x) расположен выше оси х.

5. у ≤ 0, если х ∈ [-4; -2); на этом промежутке график функции у = ƒ(x) расположен ниже оси х.

6. Функция возрастает на отрезке [-4; -1], убывает на отрезке [-1; 0] и постоянна (ни возрастает, ни убывает) на полуинтервале (0; 4].

По мере того как мы с вами будем изучать новые свойства функций, процесс чтения графика будет становиться более насыщенным, содержательным и интересным.

<<< К началу Окончание >>>