|
|
|
|
|
Глава 2. Линейная функция § 9. Линейная функция у = kx (окончание)Обратите внимание: от коэффициента k зависит угол, который построенная прямая образует с положительным направлением оси х; заметим, что этот угол отсчитывают от оси х в направлении против часовой стрелки. Если k > 0, то этот угол острый (так обстоит дело на рис. 47 с прямыми l1, l2, l3); если k < 0, то этот угол типой (так обстоит дело на рис. 47 с прямой 14). Далее, если k > 0, то чем больше k, тем больше угол.
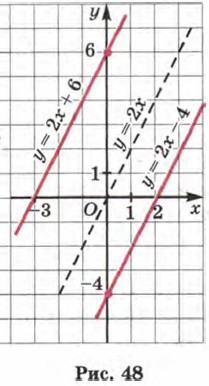
Так, на рисунке 47 для прямой l3 имеем На рисунке 48 изображены графики линейных функций у = 2х - 4, y = 2x + 6. Оба они параллельны графику линейной функции у = 2х, только первая прямая (у = 2х - 4) получается из прямой у = 2х сдвигом вниз на 4 единицы масштаба, а вторая прямая (у = 2х + 6) получается из прямой у = 2х сдвигом вверх на 6 единиц масштаба.
Справедлив следующий общий результат, который мы оформим в виде теоремы. Теорема 4.
Вследствие этого коэффициент k в записи линейной функции у = kx + m также называют угловым коэффициентом. Если k > 0, то прямая у = kx + m образует с положительным направлением оси х острый угол (см. рис. 45, а), а если k < 0, — тупой угол (см. рис. 45, б). Вопросы для самопроверки 1. Что представляет собой график линейной функции у = kx? 2. Почему в уравнении у = kx коэффициент k называют угловым? 3. Что вы можете сказать о взаимном расположении графиков функций y = kx + m и y = kx? 4. Какой угол образует прямая у = kx + m с положительным направлением оси Ох при k > 0 и при k < 0?
|
|
|




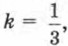 для прямой l, имеем k = 1, для прямой 12 имеем k = 2; при увеличении коэффициента k увеличивается и угол между прямой и положительным направлением оси абсцисс. Поэтому коэффициент k в записи у = kx называют угловым коэффициентом.
для прямой l, имеем k = 1, для прямой 12 имеем k = 2; при увеличении коэффициента k увеличивается и угол между прямой и положительным направлением оси абсцисс. Поэтому коэффициент k в записи у = kx называют угловым коэффициентом.