|
|
|
|
|
Глава 2. Линейная функция § 9. Линейная функция у = kxПри рассмотрении линейных функций у = kx + m особо выделяют случай, когда m = 0; тогда линейная функция принимает вид у = kx. Теорема 3.
Д о к а з а т е л ь с т в о. Осуществим его в два этапа. 1. у = kx — частный случай линейной функции, а графиком линейной функции является прямая (по теореме 2, см. с. 49); обозначим её через l. 2. Пара х = 0, у = 0 удовлетворяет уравнению у = kx, а потому точка (0; 0) принадлежит графику уравнения у = kx, т. е. прямой l. Следовательно, прямая l проходит через начало координат. Теорема доказана. Надо уметь переходить не только от аналитической модели у = kx к геометрической, но и от геометрической модели к аналитической. Рассмотрим, например, прямую на координатной плоскости хОу, изображённую на рисунке 46. Она является графиком линейной функции у = kx, нужно лишь найти значение коэффициента k. Так как
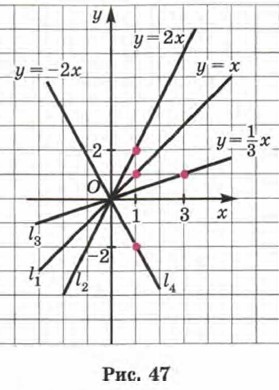
График линейной функции у = kx обычно строят так: берут точку (1; k) (если х = 1, то из равенства у = kx находим, что у = k) и проводят прямую через эту точку и начало координат. Впрочем, в случае необходимости точку (1; А) можно заменить другой точкой, более удобной. На рисунке 47 изображены графики линейных функций у = х (прямая l1), у = 2х (прямая l2)
|
|
|



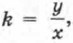 то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к её абсциссе. Прямая проходит через точку Р(3; 6), а для этой точки имеем
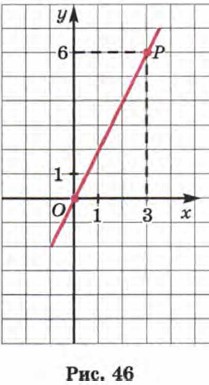
то достаточно взять любую точку на прямой и найти отношение ординаты этой точки к её абсциссе. Прямая проходит через точку Р(3; 6), а для этой точки имеем 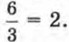 Значит, k = 2, а потому заданная прямая линия служит графиком линейной функции у = 2х.
Значит, k = 2, а потому заданная прямая линия служит графиком линейной функции у = 2х.
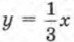 (прямая l3; ) здесь не очень удобно брать точку
(прямая l3; ) здесь не очень удобно брать точку 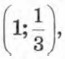 мы взяли точку (3; 1)), у = -2х (прямая l4).
мы взяли точку (3; 1)), у = -2х (прямая l4).