|
|
|
|
|
§ 1. Рациональне дроби и их свойства. Рациональные выраженияВ курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями. Целые и дробные выражения называют рациональными выражениями. Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны. Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных. Выражение вида Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью. Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
ИСААК НЬЮТОН (1643—1727) — английский физик, механик, математик и астроном. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, разработал, независимо от Лейбница, основы математического анализа. Пример 1. Найдём допустимые значения переменной в дроби
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9. Пример 2. При каком значении х значение дроби
|
|
|



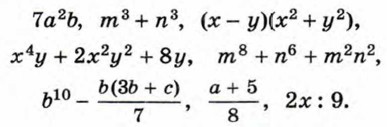
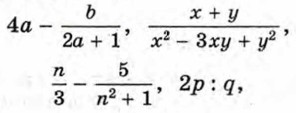
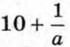 не имеет смысла при а = 0. При всех остальных значениях а это выражение имеет смысл. Выражение
не имеет смысла при а = 0. При всех остальных значениях а это выражение имеет смысл. Выражение 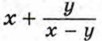 имеет смысл при тех значениях х и у, когда х ≠ у.
имеет смысл при тех значениях х и у, когда х ≠ у.
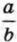 называется, как известно, дробью.
называется, как известно, дробью.
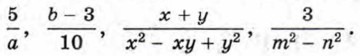

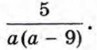
 Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а - 9) = 0.
Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а - 9) = 0.

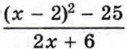 равно нулю?
равно нулю?