|
|
|
|
|
§ 4. Действительные числа Иррациональные числа (продолжение)
Число 2k2 чётное, значит, число n2 тоже чётное. Тогда и число n является чётным, т. е. числитель и знаменатель дроби Итак, десятичное измерение длин отрезков каждой точке координатной прямой, лежащей справа от начальной точки О, ставит в соответствие положительную бесконечную десятичную дробь. Наоборот, взяв произвольную положительную бесконечную десятичную дробь, мы можем найти на координатной прямой справа от точки О единственную точку А, такую, что длина отрезка О А выражается этой дробью.
Каждому действительному числу соответствует единственная точка координатной прямой, и каждой точке координатной прямой соответствует единственное действительное число. Говорят, что между множеством действительных чисел и множеством точек координатной прямой существует взаимно однозначное соответствие. Множество действительных чисел принято обозначать буквой R (от первой буквы латинского слова realis — реальный, существующий в действительности). Если A (x1) и В (х2) — две точки координатной прямой, то расстояние между этими точками, т. е. длину отрезка АВ, можно найти по формуле АВ = |х2 - х1|. Бесконечные десятичные дроби могут быть периодическими и непериодическими. Бесконечные десятичные периодические дроби представляют рациональные числа. Каждое такое число можно записать в виде отношения Таким образом,
Приведём примеры иррациональных чисел: 3,010010001... (единицы разделяются последовательно одним, двумя, тремя и т. д. нулями); -5,020022000222... (число нулей и число двоек каждый раз увеличивается на единицу). Иррациональным числом является число π, выражающее отношение длины окружности к диаметру: π = 3,1415926... . Действительные числа, записанные с помощью бесконечных десятичных дробей, сравнивают по тем же правилам, что и конечные десятичные дроби. Сравним, например, числа 2,36366... и 2,37011... . В этих положительных бесконечных десятичных дробях совпадают целые части и цифры десятых, а в разряде сотых у первой дроби число единиц меньше, чем у второй. Поэтому 2,36366... < 2,37011... . Сравним числа 0,253... и -0,149... . Первое из этих чисел положительное, а второе — отрицательное. Поэтому 0,253... > -0,149... .
|
|
|



 Предположим, что число, квадрат которого равен 2, является рациональным. Тогда это число можно представить в виде несократимои дроби
Предположим, что число, квадрат которого равен 2, является рациональным. Тогда это число можно представить в виде несократимои дроби 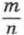 , где m — целое число, n — натуральное. Так как
, где m — целое число, n — натуральное. Так как 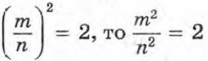 и m2 = 2n2. Число 2n2 чётное, значит, и равное ему число m2 чётное. Но тогда и само число т является чётным (если бы число m было нечётным, то и число m2 было бы нечётным). Поэтому число m можно представить в виде m = 2k, где k — целое число. Подставим 2k вместо m в равенство m2 = 2n2. Получим: (2k)2 = 2n2, 4k2 = 2n2, 2k2 = n2.
и m2 = 2n2. Число 2n2 чётное, значит, и равное ему число m2 чётное. Но тогда и само число т является чётным (если бы число m было нечётным, то и число m2 было бы нечётным). Поэтому число m можно представить в виде m = 2k, где k — целое число. Подставим 2k вместо m в равенство m2 = 2n2. Получим: (2k)2 = 2n2, 4k2 = 2n2, 2k2 = n2.
