|
|
|
|
|
§ 4. Действительные числа Иррациональные числа (окончание)Действительные числа можно складывать, вычитать, умножать и делить (при условии, что делитель отличен от нуля), причём действия над действительными числами обладают теми же свойствами, что и действия над рациональными числами. При выполнении действий над действительными числами в практических задачах их заменяют приближёнными значениями. Повышая точность, с которой берутся приближённые значения, получают более точное значение результата. Пример 4. Найдём приближённое значение суммы чисел а и b, где
а + b ≈ 0,3 + 1,7 = 2,0. Если взять приближённые значения слагаемых с точностью до 0,01, т. е. а ≈ 0,33 и b ≈ 1,71, то получим: а + b ≈ 0,33 + 1,71 = 2,04. Пример 5. Найдём длину окружности, радиус r которой равен 5 м.
l ≈ 2 • 3,14 • 5= 31,4 (м). Упражнения276. Приведите пример: а) рационального числа;
277. Верно ли, что: а) каждое рациональное число является действительным;
278. Среди чисел 279. Верно ли, что: а) 7,16 ∈ N; 7,16 ∈ Z; 7,16 ∈ Q; 7,16 ∈ R;
280. Сравните:
КАРЛ ВЕЙЕРШТРАСС (1815—1897) — немецкий математик, почётный член Петербургской академии наук. Имеет многочисленные труды по математическому анализу и другим разделам математики. С его именем связано построение теории действительных чисел на основе десятичных дробей. 281. Какое из чисел больше:
282. Сравните числа:
283. Найдите расстояние между точками М и К координатной прямой, если:
|
|
|



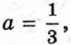 b = 1,7132... .
b = 1,7132... .
 Возьмём приближённые значения слагаемых с точностью до 0,1: а ≈ 0,3, b ≈ 1,7. Получим:
Возьмём приближённые значения слагаемых с точностью до 0,1: а ≈ 0,3, b ≈ 1,7. Получим:

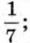 0; 0,25; -2,(3); 0,818118111... (число единиц, разделяющих восьмёрки, каждый раз увеличивается на одну); 4,2(51); 217; π укажите рациональные и иррациональные.
0; 0,25; -2,(3); 0,818118111... (число единиц, разделяющих восьмёрки, каждый раз увеличивается на одну); 4,2(51); 217; π укажите рациональные и иррациональные.



