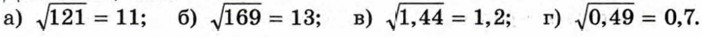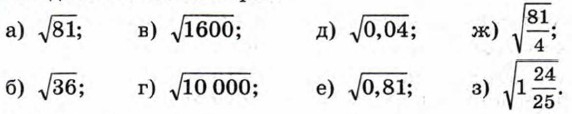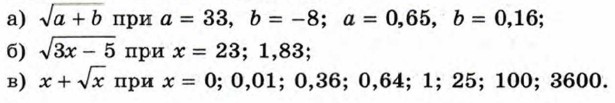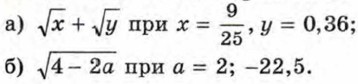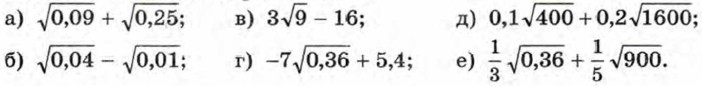Квадратные корни. Арифметический квадратный корень

Пусть площадь квадрата равна 64 см². Чему равна длина стороны этого квадрата?

Обозначим длину стороны квадрата (в сантиметрах) буквой х. Тогда площадь квадрата будет х² см². По условию площадь равна 64 см², значит, х² = 64.

Корнями уравнения х² = 64 являются числа: 8 и -8. Действительно, 8² = 64 и (-8)² = 64. Так как длина не может выражаться отрицательным числом, то условию задачи удовлетворяет только один из корней — число 8. Итак, длина стороны квадрата равна 8 см.

Корни уравнения х² = 64, т. е. числа, квадраты которых равны 64, называют квадратными корнями из числа 64.

Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.

Число 8 — неотрицательный корень уравнения х² = 64 — называют арифметическим квадратным корнем из 64. Иначе говоря, арифметический квадратный корень из 64 — это неотрицательное число, квадрат которого равен 64.

Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.

Арифметический квадратный корень из числа а обозначают √а. Знак √ называют знаком арифметического квадратного корня или знаком радикала (от латинского слова radex — корень). Выражение, стоящее под знаком корня, называют подкоренным выражением. Запись √а читают: квадратный корень из а (слово «арифметический» при чтении опускают).

Приведём примеры нахождения (или, как говорят иначе, извлечения) арифметических квадратных корней:

√4 = 2, так как 2 — число неотрицательное и 2² = 4;
√1,21 = 1,1, так как 1,1 — число неотрицательное и 1,1² = 1,21;
√0 = 0, так как 0 — число неотрицательное и 0² = 0.

√a = b, если выполняются два условия:

1) b ≥ 0; 2) b² = а.

При а < 0 выражение √a не имеет смысла.

Действительно, квадрат любого числа есть число неотрицательное. Например, не имеют смысла выражения √-25; √-3,7.

Из определения арифметического квадратного корня следует, что

при любом а, при котором выражение √a имеет смысл, верно равенство

(√a)² = a.

Упражнения

298. Докажите, что:

а) число 5 есть арифметический квадратный корень из 25;
б) число 0,3 есть арифметический квадратный корень из 0,09;
в) число -7 не является арифметическим квадратным корнем из 49;
г) число 0,6 не является арифметическим квадратным корнем из 3,6.

299. Докажите, что:

300. Найдите значение корня:

302. Найдите значение выражения:

303. Найдите значение выражения:

304. Найдите значение выражения:

Окончание >>>