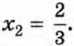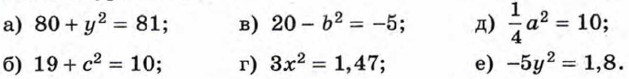|
|
|
|
|
§ 5. Арифметический квадратный корень
Уравнение х2 = аРассмотрим уравнение х2 = а, где а — произвольное число. В зависимости от числа а при решении этого уравнения возможны три случая. Если а < 0, то уравнение х2 - а корней не имеет. Действительно, не существует числа, квадрат которого был бы равен отрицательному числу. Если а = 0, то уравнение имеет единственный корень, равный нулю, так как существует единственное число 0, квадрат которого равен нулю. Если а > 0, то уравнение имеет два корня. Чтобы убедиться в этом, обратимся к графику функции у = х2 (рис. 13). Прямая у = а при а > 0 пересекает параболу у = х2 в двух точках. Обозначим абсциссы точек пересечения х1 и х2. Тогда
Например: уравнение х2 = 49 имеет корни х1 = -√49 и х2 = √49, т. е. х1 = -7 и х2 = 7;
уравнение x2 = 6,25 имеет корни x1 = -√6,25 и х2 = √6,25, т. е. х1 = -2,5 и х2 = 2,5;
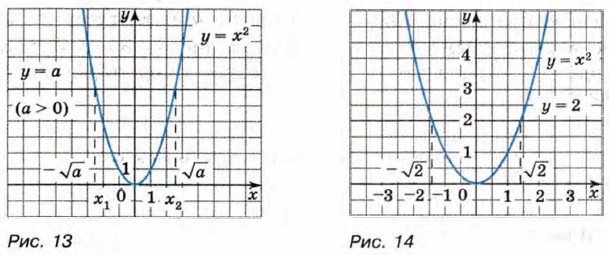
уравнение Уравнение х2 = 2 имеет корни x1 = -√2 и х2 = √2. Эти корни являются иррациональными числами, так как не существует рационального числа, квадрат которого равен 2. С помощью графика функции у = х2 легко найти приближённые значения этих корней: √2 ≈ 1,4 и -√2 ≈ -1,4 (рис. 14). Уравнения х2 =3, х2 = 5, х2 = 6,5 имеют соответственно корни -√3 и √3, -√5 и √5, -√6,5 и √6,5. Эти корни также являются иррациональными числами. Вообще, при любом а ≥ 0 уравнение х2 = а имеет неотрицательный корень √a; иными словами, какое бы число а ≥ 0 мы ни взяли, найдётся неотрицательное число, квадрат которого равен а. Это означает, что
Упражнения319. Имеет ли корни уравнение: а) х2 = 81; б) х2 = 18; в) х2 = 0; г) х2 = -25? 320. Решите уравнение:
321. Решите уравнение и с помощью графика функции у = х2 найдите приближённые значения его корней: а) х2 = 3; б) х2 = 5; в) х2 = 4,5; г) х2 = 8,5. 322. Решите уравнение:
|
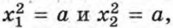значит, числа x1 и х2 — корни уравнения х2 = а. Так как х2 есть положительное число, квадрат которого равен а, то х2 является арифметическим квадратным корнем из а, т. е. х2 = √а. Так как x1 есть число, противоположное х2, то х1 = -√а.
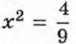имеет корни 
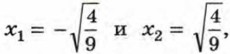т. е. 
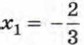и 
|
|