Функция у = √x и её график

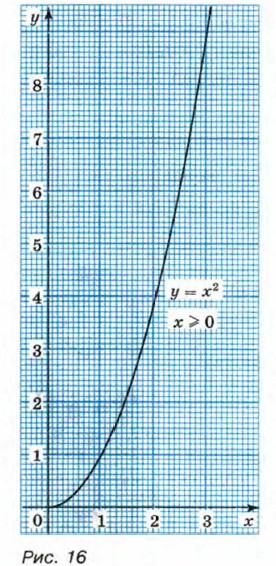
Пусть длина стороны квадрата равна а см, а его площадь равна S см². Каждому значению длины а стороны квадрата соответствует единственное значение его площади S. Зависимость площади квадрата от длины его стороны выражается формулой S = а², где а ≥ 0.

Наоборот, для каждого значения площади квадрата S можно указать соответствующее ему единственное значение длины стороны а. Зависимость длины стороны квадрата от его площади выражается формулой а = √S.

Формулами

S = а², где а ≥ 0, и а = √S

задаются функциональные зависимости между одними и теми же переменными, однако в первом случае независимой переменной является длина а стороны квадрата, а во втором — площадь S.

Если в каждом случае обозначить независимую переменную буквой х, а зависимую переменную буквой у, то получим формулы

у = х², где х ≥ 0,

y = √x.

Мы знаем, что графиком функции у = х², где х ≥ 0, является часть параболы — её правая ветвь (рис. 16). Построим теперь график функции у = √x.

Так как выражение √x имеет смысл при х ≥ 0, то областью определения функции у = √x служит множество неотрицательных чисел.

Составим таблицу значений функции у = √х (приближённые значения у для значений х, не являющихся квадратами целых чисел, можно найти с помощью калькулятора).

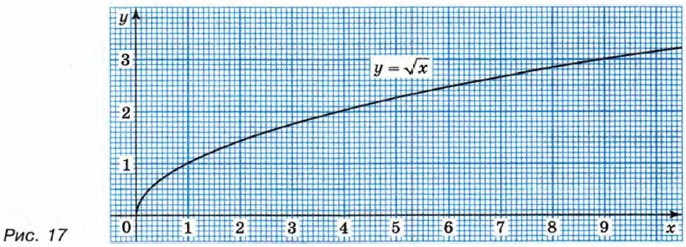
Построим в координатной плоскости точки, координаты которых указаны в таблице. Проведя от начала координат через эти точки плавную линию так, как это показано на рисунке 17, получим график функции у = √x.

Сформулируем некоторые свойства функции у = √x.

1. Если х = 0, то у = 0, поэтому начало координат принадлежит графику функции.
2. Если х > 0, то у > 0; график расположен в первой координатной четверти.
3. Большему значению аргумента соответствует большее значение функции; график функции идёт вверх.

Например: √2,6 > √1,5; √6 > √3.

Продолжение >>>