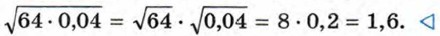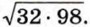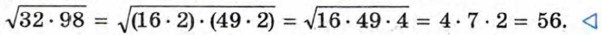|
|
|
|
|
§ 6. Свойства арифметического квадратного корня Квадратный корень из произведения и дробиСравним значения выражений
Мы видим, что
1) √a • √b ≥ 0; 2) (√a • √b)2 = ab. Так как выражения √a и √b принимают лишь неотрицательные значения, то произведение √a • √b неотрицательно. Используя свойство степени произведения, получим (√a • √b)2 = (√a)2 • (√b)2 = ab. Мы показали, что условия 1 и 2 выполняются. Значит, по определению арифметического квадратного корня при любых неотрицательных значениях а и b верно равенство √ab = √a • √b. Доказанная теорема распространяется на случай, когда число множителей под знаком корня больше двух. Например, если а ≥ 0, b ≥ 0, с ≥ 0, то Таким образом, арифметический квадратный корень обладает следующим свойством:
Рассмотрим теперь арифметический квадратный корень из дроби.
Доказательство этой теоремы аналогично доказательству теоремы 1. Проведите доказательство самостоятельно. Итак, справедливо ещё одно свойство арифметического квадратного корня:
Пример 1. Найдём значение выражения
Пример 2. Вычислим значение выражения
|
|
|



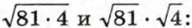
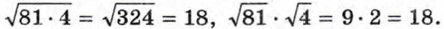
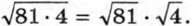 Аналогичным свойством обладает корень из произведения любых двух неотрицательных чисел.
Аналогичным свойством обладает корень из произведения любых двух неотрицательных чисел.
 Каждое из выражений √a • √b и √ab имеет смысл, так как а ≥ 0 и b ≥ 0. Покажем, что выполняются два условия:
Каждое из выражений √a • √b и √ab имеет смысл, так как а ≥ 0 и b ≥ 0. Покажем, что выполняются два условия:

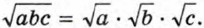
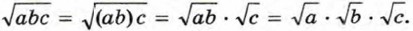
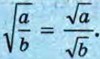
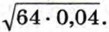
 Воспользуемся теоремой о корне из произведения:
Воспользуемся теоремой о корне из произведения: