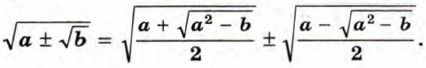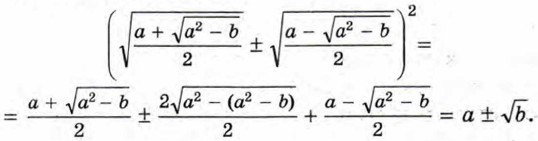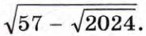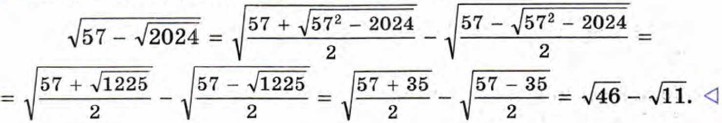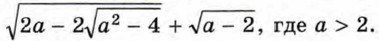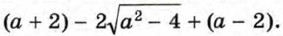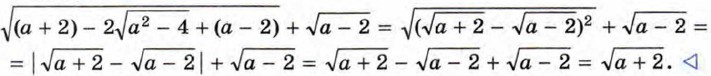|
|
|
|
|
§ 7. Применение свойств арифметического квадратного корня Преобразование двойных радикаловСторона а5 правильного пятиугольника, вписанного в круг радиуса R, вычисляется по формуле
Выражение
где а, b, с — некоторые рациональные числа. Выражение такого вида называют двойным радикалом. В преобразованиях выражений, содержащих двойные радикалы, стремятся освободиться от внешнего радикала. Это нетрудно сделать, когда выражение, стоящее под знаком радикала, можно представить в виде квадрата суммы или квадрата разности. Пример 1. Освободимся от внешнего радикала в выражении
Пример 2. Освободимся от внешнего радикала в выражении Покажем, как можно решить эту задачу, используя метод неопределённых коэффициентов.
Тогда (а + √3)2 = 61 + 28√3 и а + b√3 ≥ 0. Значит, а2 + 2ab√3 + 3b2 = 61 + 28√3. Отсюда
Выпишем все пары целых чисел (а; b), для которых ab = 14: (-14; -1), (-7; -2), (-2; -7), (-1; -14), (1; 14), (2; 7), (7; 2), (14; 1). Из этих пар выберем те, которые удовлетворяют условиям а2 + 3b2 = 61 и a + b√3 ≥ 0. Нетрудно убедиться, что такая пара единственная — это пара (7; 2). Значит,
В тех случаях, когда а ≥ 0, b ≥ 0 и разность а2 - b равна квадрату рационального числа, освободиться от внешнего радикала в выражении
В правой части этой формулы записано неотрицательное число. Покажем, что его квадрат равен а ± √b:
Пример 3. Освободимся от внешнего радикала в выражении
Освобождение от внешнего радикала используется в преобразованиях выражений с переменными, содержащих двойные радикалы. Пример 4. Упростим выражение
Получим
|
|
|



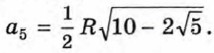
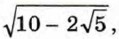 входящее в эту формулу, имеет вид
входящее в эту формулу, имеет вид
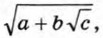
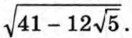
 Попытаемся представить выражение 41 - 12√5 в виде квадрата разности двух выражений. Для этого 12√5 будем рассматривать как удвоенное произведение двух выражений, а 41 как сумму их квадратов. Выражение 12√5 можно представить, например, как 2 • 6 • √5 или как 2 • 3 • 2√5. Проверка убеждает нас, что именно в первом случае сумма квадратов множителей 6 и √5 равна 41. Значит,
Попытаемся представить выражение 41 - 12√5 в виде квадрата разности двух выражений. Для этого 12√5 будем рассматривать как удвоенное произведение двух выражений, а 41 как сумму их квадратов. Выражение 12√5 можно представить, например, как 2 • 6 • √5 или как 2 • 3 • 2√5. Проверка убеждает нас, что именно в первом случае сумма квадратов множителей 6 и √5 равна 41. Значит,
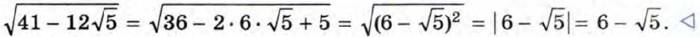
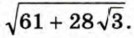
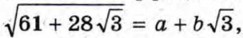 где а и b — некоторые числа.
где а и b — некоторые числа.
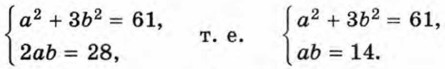
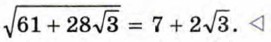
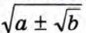 можно с помощью формулы двойного радикала:
можно с помощью формулы двойного радикала: