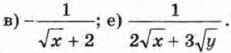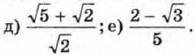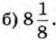|
|
|
|
|
§ 7. Применение свойств арифметического квадратного корня Преобразование выражений, содержащих квадратные корни: Ответы435. Найдите с помощью калькулятора приближённое значение выражения с точностью до 0,01:
436. Освободитесь от иррациональности в знаменателе дроби:
437. Докажите, что:
438. Докажите, что числа 2 - √3 и 2 + √3 являются взаимно обратными, а числа 2√б - 5 и 439. Среди чисел 15√3 - 4√2, 6 - √12, √80 - 5√3, √75 - 4√5, есть пара взаимно обратных чисел и пара противоположных чисел. Найдите эти пары. Упражнения для повторения440. Упростите выражение 441. Решите уравнение:
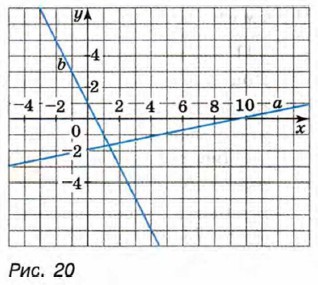
442. Площадь кольца вычисляется по формуле S = π (R2 - r2), где R — радиус внешнего круга, а r — радиус внутреннего круга. Выразите R через S и r. 443. Напишите для каждой прямой, изображённой на рисунке 20, уравнение, графиком которого является эта прямая. Контрольные вопросы и задания1. На примере выражения 3√а покажите, как можно внести множитель под знак корня. 2. На примере выражения √8a покажите, как можно вынести множитель за знак корня. 3. На примере выражении Ответы421. б) 7√2; в) 3√2; г) √3; д) 2√2. 422. д) -3√2; е) 3√2. 424. в) 6; е) 42 - 8√5. 425. а) 14; б) 8. 426. д) 6; е) -19; ж) 38; з) 2. 429. 430. 440. 20. 441. а)-1;
|
|
|



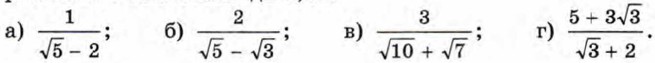
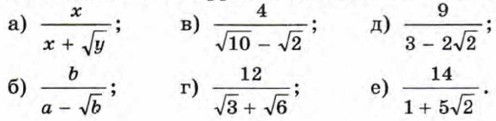
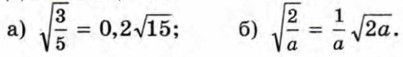
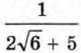 — противоположными.
— противоположными.
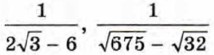
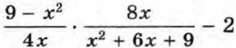 и найдите его значение при x = -2,5.
и найдите его значение при x = -2,5.
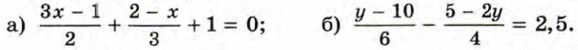
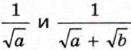 покажите, как можно освободиться от иррациональности в знаменателе дроби.
покажите, как можно освободиться от иррациональности в знаменателе дроби.