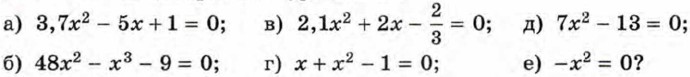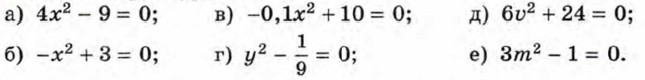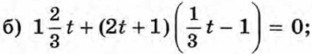|
|
|
|
|
§ 8. Квадратное уравнение и его корни Неполные квадратные уравнения (окончание)Упражнения512. Является ли квадратным уравнение:
513. Назовите в квадратном уравнении его коэффициенты:
Какие из данных уравнений являются приведёнными квадратными уравнениями? 514. Приведите примеры неполных квадратных уравнений различных видов. 515. Найдите корни уравнения:
516. Решите уравнение и укажите приближённые значения корней с точностью до 0,1 (воспользуйтесь калькулятором): а) 2х2 -17 = 0; б) 3t2 - 7,2 = 0; в) -р2 + 12,6 = 0. 517. Решите уравнение:
518. Решите уравнение:
519. Какое из данных неполных квадратных уравнений не имеет корней? 1. x2 - 19 = 0 2. x2 + 19 = 0 3. х2 - 19х = 0 4. x2 + 19x = 0 520. При каких значениях а уравнение (а - 2)х2 + 15x + а2 - 4 = 0 является неполным квадратным уравнением? Выберите верный ответ. 1. a = -1 2. a = 1 3. a = -2 4. a = 2 521. Решите уравнение:
522. Найдите корни уравнения:
523. Решите уравнение:
524. Произведение двух последовательных целых чисел в 1,5 раза больше квадрата меньшего из них. Найдите эти числа. 525. Теннисный корт представляет собой прямоугольную площадку, длина которой вдвое больше ширины, а площадь равна 800 м2. Найдите длину и ширину корта. 526. Если от квадрата отрезать треугольник площадью 59 см2, то площадь оставшейся части будет равна 85 см2. Найдите сторону квадрата.
|
|
|