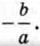|
|
|
|
|
§ 8. Квадратное уравнение и его корни Неполные квадратные уравнения (продолжение)Пример 2. Решим уравнение 4х2 + 3 = 0.
Так как квадрат числа не может быть отрицательным числом, то получившееся уравнение не имеет корней. А следовательно, не имеет корней и равносильное ему уравнение 4х2 + 3=0. Ответ: корней нет. Вообще для решения неполного квадратного уравнения вида ах2 + с = 0 при с ≠ 0 переносят его свободный член в правую часть и делят обе части уравнения на а. Получают уравнение
Пример 3. Решим уравнение 4х2 + 9х = 0.
х(4х + 9) = 0. Отсюда х = 0 или 4х + 9 = 0. Решим уравнение 4х + 9 = 0:
Ответ: х1 = 0, Вообще для решения неполного квадратного уравнения вида ах2 + bх - 0 при b ≠ 0 раскладывают его левую часть на множители и получают уравнение х (ах + b) = 0. Произведение х (ах + b) равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю: х = 0 или ах + b = 0. Решая уравнение ах + b = 0, в котором а ≠ 0, находим
Следовательно, произведение х(ах + b) обращается в нуль при х = 0 и при Значит, неполное квадратное уравнение вида ах2 + bх = 0 при b ≠ 0 всегда имеет два корня. Неполное квадратное уравнение вида ах2 = 0 равносильно уравнению х2 = 0 и поэтому имеет единственный корень 0.
|
|
|



 Перенесём свободный член в правую часть уравнения и обе части получившегося уравнения разделим на 4:
Перенесём свободный член в правую часть уравнения и обе части получившегося уравнения разделим на 4:
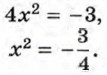

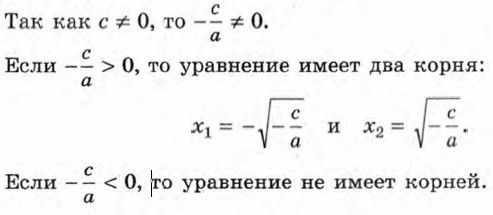
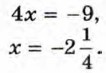
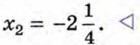
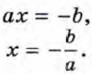
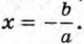 Корнями уравнения ах2 + bх = 0 являются числа 0 и
Корнями уравнения ах2 + bх = 0 являются числа 0 и