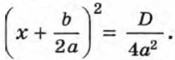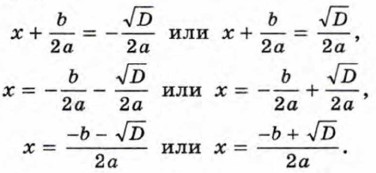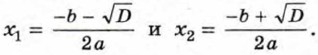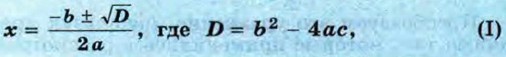|
|
|
|
|
§ 8. Квадратное уравнение и его корни Формула корней квадратного уравненияРассмотрим теперь, как решают квадратные уравнения, в которых оба коэффициента при неизвестных и свободный член отличны от нуля. Начнём с примера. Решим уравнение 7х2 - 6х - 1 = 0. Разделив обе части этого уравнения на 7, получим равносильное ему приведённое квадратное уравнение
Выделим из трехчлена Получим
Отсюда
Следовательно,
Уравнение имеет два корня: Способ, с помощью которого мы решили уравнение, называют выделением квадрата двучлена. Решение квадратных уравнений выделением квадрата двучлена часто приводит к громоздким преобразованиям. Поэтому поступают иначе. Решают уравнение в общем виде и в результате получают формулу корней. Затем эту формулу применяют при решении любого квадратного уравнения. Решим квадратное уравнение ах2 + bх + с = 0. (1) Разделив обе его части на а, получим равносильное ему приведённое квадратное уравнение
Преобразуем это уравнение, используя преобразования, аналогичные тем, которые применялись в рассмотренном примере:
Уравнение (2) равносильно уравнению (1). Число его корней зависит от знака дроби D = b2 - 4ас. Запишем уравнение (2) в виде Рассмотрим теперь различные возможные случаи в зависимости от значения D. 1) Если D > 0, то
Таким образом, в этом случае уравнение (1) имеет два корня:
Принята следующая краткая запись, которую называют формулой корней квадратного уравнения:
|
|
|



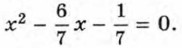
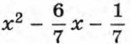 квадрат двучлена. Для этого разность
квадрат двучлена. Для этого разность 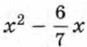 представим в виде
представим в виде 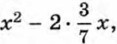 прибавим к ней выражение
прибавим к ней выражение 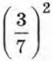 и вычтем его.
и вычтем его.
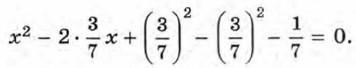
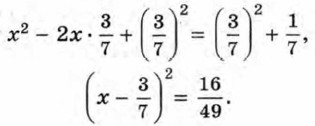
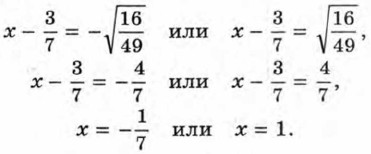
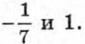
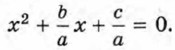
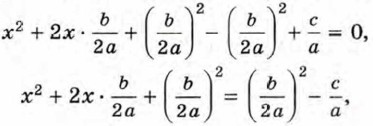
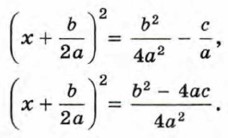
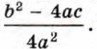 Так как а ≠ 0, то 4а2 — положительное число, поэтому знак этой дроби определяется знаком её числителя, т. е. выражения b2 - 4ас. Это выражение называют дискриминантом квадратного уравнения ах2 + bх + с = 0 («дискриминант» по-латыни — различитель). Его обозначают буквой D, т. е.
Так как а ≠ 0, то 4а2 — положительное число, поэтому знак этой дроби определяется знаком её числителя, т. е. выражения b2 - 4ас. Это выражение называют дискриминантом квадратного уравнения ах2 + bх + с = 0 («дискриминант» по-латыни — различитель). Его обозначают буквой D, т. е.