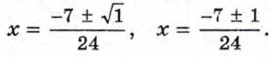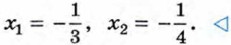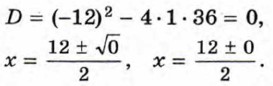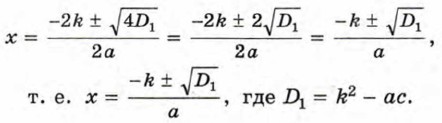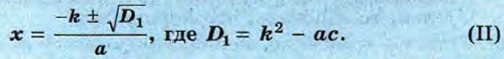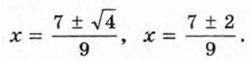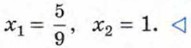|
|
|
|
|
§ 8. Квадратное уравнение и его корни
Формула корней квадратного уравнения (продолжение)2) Если D = 0, то уравнение (2) примет вид:
Отсюда
В этом случае уравнение (1) имеет один корень Формулой корней квадратного уравнения можно пользоваться и в этом случае. Действительно, при D = 0 формула (I) принимает вид
откуда
3) Если D < 0, то значение дроби
а следовательно, и уравнение (1) не имеют корней. Таким образом, в зависимости от значения дискриминанта квадратное уравнение может иметь два корня (при D > 0), один корень (при D = 0) или не иметь корней (при D < 0). При решении квадратного уравнения по формуле (I) целесообразно поступать следующим образом: 1) вычислить дискриминант и сравнить его с нулём;
Пример 1. Решим уравнение 12х2 + 7х + 1 = 0.
D = 72 - 4 • 12 • 1 = 1, D > 0. Применим формулу корней квадратного уравнения:
Ответ: Пример 2. Решим уравнение х2 - 12х + 36 = 0.
Ответ: 6. Пример 3. Решим уравнение 7х2 - 25х + 23 = 0.
D = (-25)2 - 4 • 7 • 23 = 625 - 644, D < 0. Ответ: корней нет. Из формулы (I) можно получить другую формулу, которой удобно пользоваться при решении квадратных уравнений с чётным вторым коэффициентом. Рассмотрим квадратное уравнение ах2 + 2kx + с = 0. Найдём его дискриминант: D = 4k2 - 4ас = 4(k2 - ас). Очевидно, что число корней уравнения зависит от знака выражения k2 - ас. Обозначим это выражение через D1. Если D1 ≥ 0, то по формуле корней квадратного уравнения получим
Значит, если квадратное уравнение имеет вид ах2 + 2kx + с = 0, то при D1 ≥ 0 его корни могут быть найдены по формуле
Если D1 < 0, то уравнение корней не имеет. Пример 4. Решим уравнение 9х2 - 14х + 5 = 0.
Ответ:
|
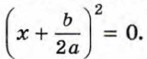
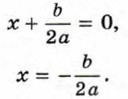
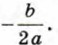
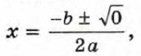
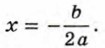
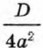отрицательно и поэтому уравнение
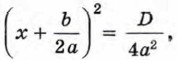
Найдём дискриминант:
|
|