|
|
|
|
|
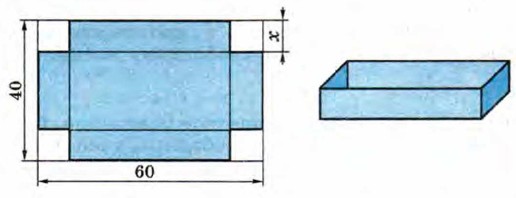
§ 8. Квадратное уравнение и его корни Решение задач с помощью квадратных уравнений (продолжение)Упражнения559. Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа. 560. Найдите периметр прямоугольника, длина которого на 4 см больше ширины, а площадь равна 60 см2. 561. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определите длину изгороди, если известно, что площадь участка равна 1200 м2. 562. Периметр прямоугольника равен 62 м. Найдите его стороны, если площадь прямоугольника равна 210 м2. 563. Найдите катеты прямоугольного треугольника, если известно, что их сумма равна 23 см, а площадь данного треугольника равна 60 см2. 564. Произведение двух последовательных натуральных чисел больше их суммы на 109. Найдите эти числа. 565. Площадь доски прямоугольной формы равна 4500 см2. Доску распилили на две части, одна из которых представляет собой квадрат, а другая — прямоугольник. Найдите сторону получившегося квадрата, если длина отпиленного прямоугольника равна 120 см. 566. От прямоугольного листа картона длиной 26 см отрезали с двух сторон квадраты, сторона каждого из которых равна ширине листа. Площадь оставшейся части равна 80 см2. Найдите ширину листа картона. Покажите, что задача имеет два решения, и для каждого случая сделайте чертеж (в масштабе 1 : 2). 567. В прямоугольном треугольнике один из катетов на 3 см меньше гипотенузы, а другой — на 6 см меньше гипотенузы. Найдите гипотенузу. 568. В кинотеатре число мест в ряду на 8 больше числа рядов. Сколько рядов в кинотеатре, если всего в нём имеется 884 места? 569. Старинная задача. Стая обезьян забавляется. Восьмая часть их в квадрате резвится в лесу. Остальные двенадцать кричат на вершине холма. Скажи мне, сколько всего обезьян? 570. Старинная задача. Квадрат пятой части обезьян, уменьшенной на 3, спрятался в гроте. Одна обезьяна, влезшая на дерево, была видна. Сколько было обезьян? 571. Число диагоналей р выпуклого многоугольника вычисляется 572. При розыгрыше первенства школы по футболу было сыграно 36 матчей, причём каждая команда сыграла с каждой по одному разу. Сколько команд участвовало в розыгрыше? 573. В шахматном турнире было сыграно 45 партий. Определите число участников турнира, если известно, что каждый участник сыграл с каждым по одной партии. 574. От прямоугольного листа картона, длина которого равна 60 см, а ширина — 40 см, отрезали по углам равные квадраты и из оставшейся части склеили открытую коробку. Найдите сторону квадрата, если известно, что площадь основания коробки равна 800 см2.
575. Найдите три последовательных целых числа, сумма квадратов которых равна 869.
|
|
|



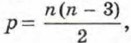 где n — число сторон. В каком выпуклом многоугольнике диагоналей на 25 больше, чем сторон?
где n — число сторон. В каком выпуклом многоугольнике диагоналей на 25 больше, чем сторон?