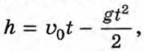Решение задач с помощью квадратных уравнений

Многие задачи в математике, физике, технике решаются с помощью квадратных уравнений.

Задача 1. Найдём катеты прямоугольного треугольника, если известно, что один из них на 4 см меньше другого, а гипотенуза равна 20 см.

Пусть меньший катет равен х см. Тогда больший катет равен (х + 4) см. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, т. е.

х² + (х + 4)² = 20².

Упростим это уравнение:

х² + х² + 8х + 16 = 400,
2х² + 8х- 384= 0,
х² + 4х - 192 = 0.

Решив полученное квадратное уравнение, найдём, что

x₁ = -16, х₂ = 12.

По смыслу задачи значение х должно быть положительным числом. Этому условию удовлетворяет только второй корень, т. е. число 12.

Ответ: 12 см, 16 см.

Задача 2. Тело брошено вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд оно окажется на высоте 60 м?

Из курса физики известно, что если не учитывать сопротивление воздуха, то высота h (м), на которой брошенное вертикально вверх тело окажется через t (с), может быть найдена по формуле

где υ₀ (м/с) — начальная скорость, g — ускорение свободного падения, приближённо равное 10 м/с².

Подставив значения h и υ₀ в формулу, получим

60 = 40t - 5t².

Отсюда

5t² - 40t + 60 = 0,
t² - 8t+ 12 = 0.

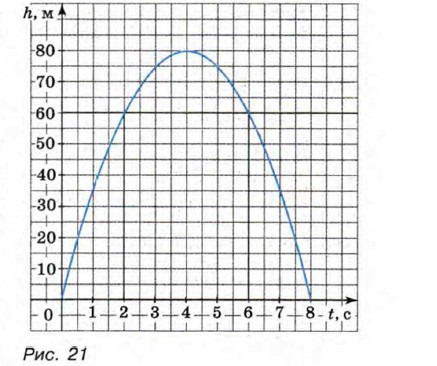
Решив полученное квадратное уравнение, найдём, что t₁ = 2, t₂ = б.

На рисунке 21 дан график зависимости h от t, где h = 40t - 5t². Из графика видно, что тело, брошенное вертикально вверх, в течение первых 4 с поднимается вверх до высоты 80 м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды: через 2 с и через 6 с после бросания.

Условию задачи удовлетворяют оба найденных корня. Значит, ответ на вопрос задачи таков: на высоте 60 м тело окажется через 2 с и через 6 с.

Продолжение >>>