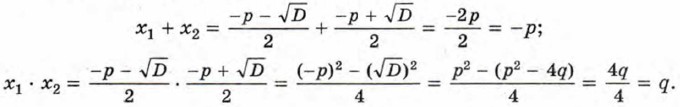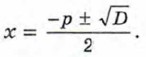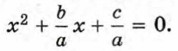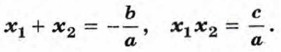Теорема Виета

Приведённое квадратное уравнение х² - 7х + 10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Мы видим, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Докажем, что таким свойством обладает любое приведённое квадратное уравнение, имеющее корни.

ТЕОРЕМА
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Рассмотрим приведённое квадратное уравнение. Обозначим второй коэффициент буквой р, а свободный член буквой q:

х² + рх + q = 0.

Дискриминант этого уравнения D равен р² - 4q.

Пусть D > 0. Тогда это уравнение имеет два корня:

Найдём сумму и произведение корней:

Итак,

х₁ + х₂ = -р, x₁ • х₂ = q.

Теорема доказана.

При D = 0 квадратное уравнение х² + рх + q = 0 имеет один корень. Если условиться считать, что при D = 0 квадратное уравнение имеет два равных корня, то теорема будет верна и в этом случае. Это следует из того, что при D = 0 корни уравнения также можно вычислять по формуле

Доказанная теорема называется теоремой Виета по имени знаменитого французского математика Франсуа Виета.

Используя теорему Виета, можно выразить сумму и произведение корней произвольного квадратного уравнения через его коэффициенты.

Пусть квадратное уравнение ах² + bх + с = 0 имеет корни x₁ и х₂. Равносильное ему приведённое квадратное уравнение имеет вид

По теореме Виета

Справедливо утверждение, обратное теореме Виета:

ТЕОРЕМА
Если числа m и n таковы, что их сумма равна -р, а произведение равно q, то эти числа являются корнями уравнения x² + рх + q = 0.

По условию m + n=-р, а mn = q. Значит, уравнение х² + рх + q = 0 можно записать в виде

х² - (m + n) х + mn = 0.

Подставив вместо x число m, получим:

m² - (m + n)m + mn = m² - m² - mn + mn = 0.

Значит, число m является корнем уравнения.

Аналогично можно показать, что число n также является корнем уравнения.

Рассмотрим примеры применения теоремы Виета и теоремы, обратной теореме Виета.

Продолжение >>>