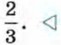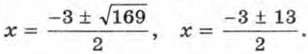|
|
|
|
|
§ 8. Квадратное уравнение и его корни Теорема Виета (продолжение)
ФРАНСУА ВИЕТ (1540—1603) — французский математик, ввёл систему алгебраических символов, разработал основы элементарной алгебры. Он был одним из первых, кто числа стал обозначать буквами, что существенно развило теорию уравнений. Пример 1. Найдём сумму и произведение корней уравнения 3х2 - 5х + 2 = 0.
По теореме, обратной теореме Виета, можно проверять, правильно ли найдены корни квадратного уравнения. Пример 2. Решим уравнение х2 + 3х - 40 = 0 и выполним проверку по теореме, обратной теореме Виета.
D = 32 + 4 • 40 = 169. По формуле корней квадратного уравнения получаем
Отсюда х1 = -8, х2 = 5. Покажем, что корни уравнения найдены правильно. В уравнении х2 + 2х - 40 = 0 коэффициент р равен 3, а свободный член q равен -40. Сумма найденных чисел -8 и 5 равна -3, а их произведение равно -40. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения х2 + 3х - 40 = 0. Пример 3. Найдём подбором корни уравнения х2 - х - 12 = 0.
x1 + х2 = 1 и х1 • х2 = —12. Если х1 и х2 — целые числа, то они являются делителями числа -12. Учитывая также, что сумма этих чисел равна 1, нетрудно догадаться, что x1 = -3 и х2 = 4. Упражнения580. Найдите сумму и произведение корней уравнения:
581. Решите уравнение и выполните проверку по теореме, обратной теореме Виета:
582. Найдите корни уравнения и выполните проверку по теореме, обратной теореме Виета:
583. Найдите подбором корни уравнения:
584. Найдите подбором корни уравнения: а) х2 + 16х + 63 = 0; б) х2 + 2х - 48 = 0. 585. В уравнении х2 + рх - 35 = 0 один из корней равен 7. Найдите другой корень и коэффициент р. 586. Один из корней уравнения х2 - 13х + q = 0 равен 12,5. Найдите другой корень и коэффициент q. 587. Один из корней уравнения 5х2 + bх + 24 = 0 равен 8. Найдите другой корень и коэффициент b. 588. Один из корней уравнения 10х2 - 33х + с = 0 равен 5,3. Найдите другой корень и коэффициент с. 589. Разность корней квадратного уравнения х2 - 12х + q = 0 равна 2. Найдите q. 590. Разность корней квадратного уравнения х2 + х + с = 0 равна 6. Найдите с.
|
|
|




 Дискриминант D = 25 - 4 • 3 • 2 = 1 — положительное число. Значит, уравнение имеет корни. Эти же корни имеет приведённое квадратное уравнение
Дискриминант D = 25 - 4 • 3 • 2 = 1 — положительное число. Значит, уравнение имеет корни. Эти же корни имеет приведённое квадратное уравнение 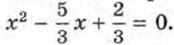 Значит, сумма корней уравнения 3х2 - 5х + 2 = 0 равна
Значит, сумма корней уравнения 3х2 - 5х + 2 = 0 равна 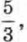 а произведение равно
а произведение равно