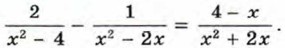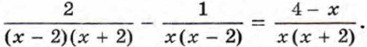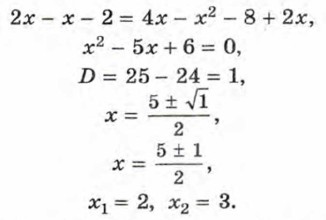|
|
|
|
|
§ 9. Дробные рациональные уравнения Решение дробных рациональных уравненийВ уравнениях
левая и правая части являются рациональными выражениями. Такие уравнения называют рациональными уравнениями. Рациональное уравнение, в котором и левая и правая части являются целыми выражениями, называют целым. Рациональное уравнение, в котором левая или правая часть является дробным выражением, называют дробным. Так, уравнение 2х + 5 = 3(8 - х) целое, а уравнения Пример 1. Решим целое уравнение
3(х - 1) + 4х = 5х. Решив его, найдём, что х = 1,5. Пример 2. Решим дробное рациональное уравнение
x(x - 3) + x - 5 = x + 5. (2) Понятно, что каждый корень уравнения (1) является корнем уравнения (2). Но уравнение (2) может быть не равносильно исходному, так как мы умножили обе его части не на число, отличное от нуля, а на выражение, содержащее переменную, которое может обращаться в нуль. Поэтому не каждый корень уравнения (2) обязательно окажется корнем уравнения (1). Упростив уравнение (2), получим квадратное уравнение х2 - 3х - 10= 0. Его корни — числа -2 и 5. Проверим, являются ли числа -2 и 5 корнями уравнения (1). При х = -2 общий знаменатель х(х- 5) не обращается в нуль. Значит, число -2 — корень уравнения (1). При х = 5 общий знаменатель обращается в нуль и выражения Итак, корнем уравнения (1) служит только число -2.
Пример 3. Решим уравнение
Общий знаменатель дробей x(x - 2)(х + 2). Умножив обе части уравнения на общий знаменатель дробей, получим 2х - (х + 2) = (4 - х)(х - 2). Отсюда
Если x = 2, то х(х - 2)(х + 2) = 0; если х = 3, то х(х - 2)(х + 2) ≠ 0. Значит, корнем исходного уравнения является число 3. Ответ: 3.
|
|
|



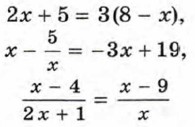
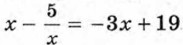 и
и 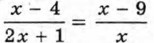 дробные рациональные.
дробные рациональные.
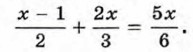
 Умножим обе части уравнения на наименьший общий знаменатель входящих в него дробей, т. е. на число 6. Получим уравнение, равносильное данному, не содержащее дробей:
Умножим обе части уравнения на наименьший общий знаменатель входящих в него дробей, т. е. на число 6. Получим уравнение, равносильное данному, не содержащее дробей:

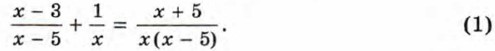
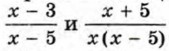 теряют смысл. Поэтому число о не является корнем уравнения (1).
теряют смысл. Поэтому число о не является корнем уравнения (1).