|
|
|
|
|
Дополнительные упражнения к главе III Дополнительные упражнения к § 8 (продолжение)663. Периметр прямоугольника равен 28 см, а сумма площадей квадратов, построенных на двух смежных сторонах прямоугольника, равна 116 см2. Найдите стороны прямоугольника. 664. Фотографическая карточка размером 12x18 см наклеена на лист так, что получилась рамка одинаковой ширины. Определите ширину рамки, если известно, что фотокарточка вместе с рамкой занимает площадь 280 см2. 665. Цветочная клумба, имеющая форму прямоугольника, окружена дерновым бордюром, ширина которого всюду одинакова. Клумба вместе с бордюром образует прямоугольник, длина которого 4,5 м, а ширина 2,5 м. Найдите ширину бордюра, если известно, что его площадь равна 3,25 м2. 666. Старинная задача. Некто купил лошадь и спустя некоторое время продал её за 24 пистоля. При этом он потерял столько процентов, сколько стоила сама лошадь. Спрашивается: за какую сумму он её купил? 667. Дно ящика — прямоугольник, ширина которого в 2 раза меньше его длины. Высота ящика 0,5 м. Найдите объём ящика, если известно, что площадь его дна на 1,08 м2 меньше площади боковых стенок. 668. Имеется лист картона прямоугольной формы, длина которого в 1,5 раза больше его ширины. Из него можно изготовить открытую коробку объёмом 6080 см3, вырезав по углам картона квадраты со стороной 8 см. Найдите размеры — длину и ширину листа картона. 669. Разность кубов двух последовательных натуральных чисел равна 919. Найдите эти числа. 670. Разность кубов двух последовательных нечётных натуральных чисел равна 866. Найдите эти числа. 671. Решите уравнение и выполните проверку по теореме, обратной теореме Виета:
672. Найдите b и решите уравнение: а) 2х2 + bх - 10 = 0, если оно имеет корень 5;
б) 3х2 + bх + 24 = 0, если оно имеет корень 3;
в) (b - 1)х2 - (b + 1)х = 72, если оно имеет корень 3;
г) (b - 5)х2 - (b - 2)х + b = 0, если оно имеет корень 673. Докажите, что уравнение 7х2 + bх - 23 = 0 при любых значениях b имеет один положительный и один отрицательный корень. 674. Докажите, что уравнение 12x2 + 70x + а2 + 1 = 0 при любых значениях а не имеет положительных корней. 675. Докажите, что если сумма коэффициентов квадратного уравнения ах2 + bх + с = 0 равна нулю, то один из корней уравнения равен 1. Используя это свойство, решите уравнение: а) 2x2 - 41x + 39 = 0; б) 17x2 + 243x - 260 = 0. 676. Разность корней уравнения 3х2 + bх + 10 = 0 равна 677. Один из корней уравнения 5x2 - 12x +с = 0 в 3 раза больше другого. Найдите с. 678. Частное корней уравнения 4x2 + bх - 27 = 0 равно -3. Найдите b. 679. Квадрат разности корней уравнения x2 + рх + 90 = 0 равен 81. Найдите р. 680. Разность квадратов корней уравнения 2x2 - 5x + с = 0 равна 0,25. Найдите с. 681. Один из корней уравнения 4x2 + bх + с = 0 равен 0,5, а другой — свободному члену. Найдите b и с. 682. Известно, что коэффициенты бис уравнения х2 + бх + с = 0, где с ≠ 0, являются его корнями. Найдите b и с. 683. Выразите через р и q сумму квадратов корней уравнения х2 + рх + q = 0.
|
|
|



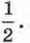
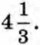 Найдите b.
Найдите b.