|
|
|
|
|
Дополнительные упражнения к главе III Дополнительные упражнения к § 8: Ответы684. Известно, что сумма квадратов корней уравнения х2 - 15х + q = 0 равна 153. Найдите q. 685. Квадрат разности корней уравнения х2 + рх + 405 = 0 равен 144. Найдите р. 686. Известно, что х1 и х2 — корни уравнения 3х2 + 2х + k = 0, причём 2x1 = -3х2. Найдите k. 687. Известно, что х1 и х2 — корни уравнения х2 - 8х + k = 0, причём 3х1 + 4х2 = 29. Найдите k. 688. Зная, что уравнение х2 + px + q= 0 имеет корни x1 и х2, составьте квадратное уравнение, имеющее корни: а) 3x1 и 3х2; б) х1 + 2 и х2 + 2. Известно, что уравнение х2 + рх + q = 0 имеет корни x1 и х2. Составьте квадратное уравнение, корнями которого являются числа Ответы650. а) 0; 1; б) 0; 6,8; в)-1,2; 1,2; г) 0. 654. 655. а)-1,2; 0,2; 660. 10, 11, 12, 13, 14 или -2, -1, 0, 1, 2. 661. -2, 0, 2 или 6, 8, 10. 662. 7 и 8. 663. 4 см и 10 см. 664. 1 см. 665. 0,25 м. 666. 60 или 40 пистолей. 667. 0,36 м3 или 0,81 м3. 668. 54 см и 36 см. 669. 18 и 17. 670. 13 и 11. 671. a) 2√2; 3√2; б) -6√3; 4л/3; в) 3- √2; 3 + √2; г) 5 - 3√2; 5 + 3√2. 678. b = ±12. 679. 21 или -21. 680. с = 3,12. 681. b = -2, с = 0. 682. b = 1, с = -2. 684. 36. 685. 42 или -42. 688. а) х2 + 3рх + 9q = 0; б) х2 + (р - 4) х + (q - 2р + 4) = 0. 689. qx2 — (р — 2q)х + q = 0.
|
|
|



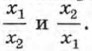
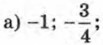 б)-8; 7; в)-7; 8; г) 1,6; 2;
б)-8; 7; в)-7; 8; г) 1,6; 2; 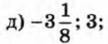
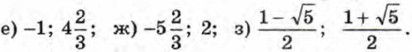
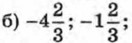
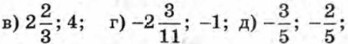 е) -1; 1; ж) -2,5; 2,5; з) при любом х.
е) -1; 1; ж) -2,5; 2,5; з) при любом х.