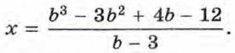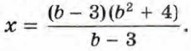|
|
|
|
|
§ 9. Дробные рациональные уравнения Уравнения с параметромКаждое из уравнений 7x = 5, -3x = 5, 0х = 5 имеет вид ах = 5, где а — некоторое число. Первое уравнение, в котором а = 7, имеет корень Вообще, уравнение вида ах = 5 при а ≠ 0 имеет единственный корень Рассматривая уравнение ах = 5, мы придавали буквам а и х различный смысл, считая, что буквой х обозначено неизвестное число, а буквой а — некоторое фиксированное число. В таких случаях говорят, что а является параметром, а ах = 5 — уравнение с параметром. Для уравнения ах = 5 мы выяснили, что при любом значении параметра а, не равном нулю, корень уравнения можно найти по формуле Вообще решить уравнение с параметром — это значит показать, каким образом для любого значения параметра можно найти соответствующее множество корней уравнения, если корни существуют, или установить, что при этом значении параметра корней нет. Рассмотрим примеры. Пример 1. Решим уравнение bх - 3х= b3 - 3b2 + 4b - 12 с параметром b.
(b - 3)х = b3 - 3b2 + 4b - 12. Мы имеем линейное уравнение, число корней которого зависит от того, отличен ли от нуля коэффициент при х или равен нулю. Если b - 3 ≠ 0, т. е. b ≠ 3, то уравнение имеет единственный корень
Разложив числитель дроби на множители, получим, что
Отсюда х = b2 + 4. Если b - 3 = 0, т. е. b = 3, то уравнение принимает вид 0x = 0. В этом случае любое число является корнем уравнения. Итак, мы нашли, что при b ≠ 3 уравнение имеет единственный корень b2 + 4, а при b = 3 любое число является корнем уравнения.
|
|
|



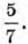 Второе уравиение, в котором а = -3, имеет корень
Второе уравиение, в котором а = -3, имеет корень 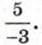 Третье уравнение, в котором а = 0, не имеет корней.
Третье уравнение, в котором а = 0, не имеет корней.
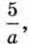 а при а = 0 не имеет корней.
а при а = 0 не имеет корней.
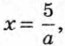 при а = 0 это уравнение корней не имеет. В таких а случаях говорят, что мы решили уравнение с параметром.
при а = 0 это уравнение корней не имеет. В таких а случаях говорят, что мы решили уравнение с параметром.
 Вынесем в левой части уравнения множитель х за скобки. Получим
Вынесем в левой части уравнения множитель х за скобки. Получим