|
|
|
|
|
§ 9. Дробные рациональные уравнения
Уравнения с параметром (продолжение)Пример 2. Решим уравнение ах2 + (а2 - 1)х + (а - 1)2 = 0 с параметром а.
Если а = 0, то данное уравнение обращается в линейное уравнение -х +1 = 0, которое имеет единственный корень х = 1. Пусть а ≠ 0. Тогда мы имеем квадратное уравнение ах2 + (а2 - 1)x - (а - 1)2 = 0. Найдём его дискриминант: D = (а2 - 1)2 - 4а(а - 1)2 = (а - 1)2((а + 1)2 - 4а) = (а - 1)4. Так как D ≥ 0 при любом значении а, то это уравнение при любом а имеет корни. Если а = 1, то D = 0, и это уравнение имеет единственный корень. Найти его можно, подставив в уравнение вместо а число 1. Получим х4 = 0. Отсюда х = 0. Если а ≠ 1, то D > 0, и уравнение имеет два корня:
Итак, мы нашли, что данное уравнение имеет корень 1 при а = 0, корень 0 при а = 1, корни 1 - а и Упражнения640. Какие случаи надо выделить при решении уравнения bх + 2х = 3b + 6 с параметром b? Найдите корни уравнения в каждом из этих случаев. 641. Решите относительно у уравнение: а) ру - р - 1 = 0;
642. Решите уравнение с параметром ах - 2х = а3 - 2а2 - 9а + 18. 643 Решите уравнение с параметром b: 2х2 - 4х + b = 0. 644. Решите относительно х уравнение: а) х2 - 5ах + 4а2 = 0; б) 3х2 - 10аx + 3а2 = 0.
|
Данное уравнение при а = 0 является линейным, а при а ≠ 0 — квадратным. Рассмотрим каждый из этих случаев.
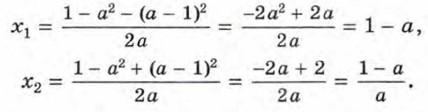
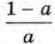при а ≠ 0 и а ≠ 1. 
|
|