|
|
|
|
|
§ 10. Числовые неравенства и их свойства Числовые неравенстваВ этой главе вы познакомитесь со свойствами числовых неравенств, научитесь применять их при сравнении выражений, доказательстве неравенств. Впервые вы встретитесь с понятиями абсолютной и относительной погрешностей, точности приближения, узнаете, какой смысл имеет запись а ± h, которая часто используется на продукции разного рода. Основное содержание главы составляет решение неравенств, сводящихся к виду ах + b > 0 или к виду ах + b < 0, и их систем. Неравенства такого вида решают аналогично тому, как решают уравнения вида ах + b = 0, но при этом следует учитывать знак коэффициента а. Геометрическая интерпретация множеств решений неравенств и вводимые понятия пересечения и объединения множеств помогут вам при решении различных задач. Мы можем сравнить любые числа а и b и результат сравнения записать в виде равенства или неравенства, используя знаки = , <, >. Для произвольных чисел а и b выполняется одно и только одно из соотношений: а = b, а < b, а > b. Рассмотрим примеры. 1. Сравним обыкновенные дроби
Так как 35 > 32, то 2. Сравним десятичные дроби 3,6748 и 3,675. Цифры в разрядах единиц, десятых и сотых совпадают, а в разряде тысячных в первой дроби стоит цифра 4, а во второй — цифра 5. Так как 4 < 5, то 3,6748 < 3,675. 3. Сравним обыкновенную дробь 4. Сравним отрицательные числа -15 и -23. Модуль первого числа меньше модуля второго. Значит, первое число больше второго, т. е. -15 > -23. В зависимости от конкретного вида чисел мы использовали тот или иной способ сравнения. Однако удобно иметь такой способ сравнения чисел, который охватывает все случаи. Он заключается в том, что составляют разность чисел и выясняют, является ли она положительным числом, отрицательным числом или нулём. Этот способ сравнения чисел основан на следующем определении:
Заметим, что если разность а - b равна нулю, то числа а и b равны.
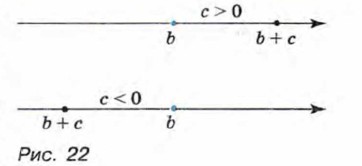
На координатной прямой большее число изображается точкой, лежащей правее, а меньшее — точкой, лежащей левее. Действительно, пусть а и b — некоторые числа. Обозначим разность а - b буквой с. Так как а - b = с, то а = b + с. Если с — положительное число, то точка с координатой b + с лежит правее точки с координатой Ь, а если с — отрицательное число, то левее (рис. 22). Значит, если а > b, то точка с координатой а лежит правее точки с координатой b, а если а < b — левее. Покажем, как приведённое определение используется при решении задач. Пример 1. Докажем, что при любых значениях переменной а верно неравенство (а - 3)(а - 5) < (а - 4)2.
(а - 3) (а - 5) - (а - 4)2 =
При любом а рассматриваемая разность отрицательна и, следовательно. верно неравенство (а - 3)(а - 5) < (а - 4)2.
|
|
|



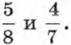 Для этого приведём их к общему знаменателю:
Для этого приведём их к общему знаменателю:
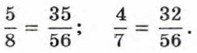
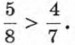
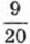 и десятичную дробь 0,45. Обратив дробь
и десятичную дробь 0,45. Обратив дробь 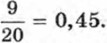
 Составим разность левой и правой частей неравенства и преобразуем её:
Составим разность левой и правой частей неравенства и преобразуем её:
