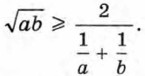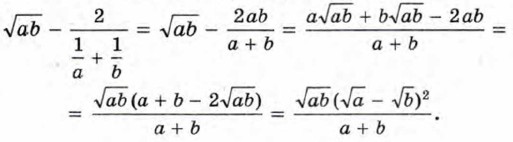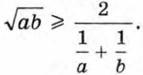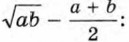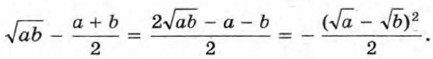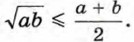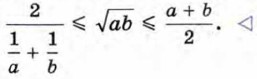|
|
|
|
|
§ 10. Числовые неравенства и их свойства Числовые неравенства (продолжение)Пример 2. Пусть а и b — положительные числа. Как известно, число
Преобразуем разность левой и правой частей этого неравенства:
При a > 0 и b > 0 рассматриваемая разность неотрицательна и, следовательно, верно неравенство
Рассмотрим теперь разность
При а > 0 и b > 0 составленная разность либо является отрицательным числом, либо равна нулю и, значит, верно неравенство
Итак, мы доказали, что если а > 0 и b > 0, то
Упражнения724. Сравните числа а и b, если: а) а - b = -0,001; б) а - b = 0; в) а - b = 4,3. 725. Известно, что а < b. Может ли разность а - Ъ выражаться числом 3,72? -5? 0? 726. Даны выражения За (а + 6) и (3а + 6) (а + 4). Сравните их значения при а = -5; 0; 40. Докажите, что при любом а значение первого выражения меньше значения второго. 727. Даны выражения 46(b + 1) и (2b + 7) (2b - 8). Сравните их значения при b = -3; -2; 10. Можно ли утверждать, что при любом значении 6 значение первого выражения больше, чем значение второго? 728. Докажите, что при любом значении переменной верно неравенство:
729. Докажите неравенство:
730. Верно ли при любом х неравенство: а) 4x(x + 0,25) > (x + 3)(x - 3);
|
|
|



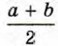 называется средним арифметическим чисел а и b, число
называется средним арифметическим чисел а и b, число 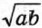 — средним геометрическим, число
— средним геометрическим, число 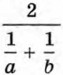 — средним гармоническим. Докажем, что среднее арифметическое, среднее геометрическое и среднее гармоническое положительных чисел а и b связаны следующим соотношением:
— средним гармоническим. Докажем, что среднее арифметическое, среднее геометрическое и среднее гармоническое положительных чисел а и b связаны следующим соотношением:
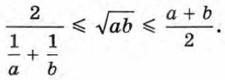
 Докажем сначала, что
Докажем сначала, что