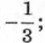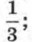|
|
|
|
|
§ 10. Числовые неравенства и их свойства Свойства числовых неравенств (продолжение)
Приведём пример использования рассмотренных свойств неравенств. Пример. Оценим периметр равностороннего треугольника со стороной а мм, если известно, что 54,2 < а < 54,3.
54,2 • 3 < 3а < 54,3 • 3, 162,6 < 3а < 162,9. Значит, периметр Р данного треугольника больше 162,6 мм, но меньше 162,9 мм. Упражнения746. Отметьте на координатной прямой точки, имеющие координаты а, b, с, d и е, если а < b, с > b, с < d, а > e. 747. Пусть m, n, р и q — некоторые числа, причём m > р, n > m, n < q. Сравните, если это возможно, числа р и n, р и q, q и m. При сравнении чисел воспользуйтесь координатной прямой. 748. Известно, что а < b. Сравните, если возможно, а и b + 1, a - 3 и b, а - 5 и b + 2, а + 4 и b - 1. 749. Какими числами (положительными, отрицательными) являются а и b, если известно, что верны неравенства:
750. Используя свойства неравенств, запишите верное неравенство, которое получится, если: а) к обеим частям неравенства 18 > -7 прибавить число -5; число 2,7; число 7;
751. Известно, что а < b. Используя свойства неравенств, запишите верное неравенство, которое получится, если: а) к обеим частям этого неравенства прибавить число 4;
752. Известно, что а < b. Поставьте вместо звёздочки знак < или > так, чтобы получилось верное неравенство:
753. Каков знак числа а, если известно, что: а) 5а < 2а; б) 7а > 3а; в) -3а < 3а; г) -12а > -2а?
|
|
|



 Разделим обе части неравенства а < b на положительное число аb:
Разделим обе части неравенства а < b на положительное число аb: 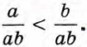 Сократив дроби, получим, что
Сократив дроби, получим, что 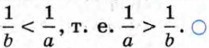
 Периметр равностороннего треугольника со стороной а вычисляется по формуле Р = 3а. Умножим на 3 обе части каждого из неравенств 54,2 < а и а < 54,3 и запишем результат в виде двойного неравенства:
Периметр равностороннего треугольника со стороной а вычисляется по формуле Р = 3а. Умножим на 3 обе части каждого из неравенств 54,2 < а и а < 54,3 и запишем результат в виде двойного неравенства: