Свойства числовых неравенств

Рассмотрим некоторые свойства числовых неравенств.

ТЕОРЕМА 1
Если а > b, то b < а; если а < b, то b > а.

Действительно, если разность а - b — положительное число, то разность b - а — отрицательное число, и наоборот.

ТЕОРЕМА 2
Если а < b и b < с, то а < с.

Докажем, что разность а - с — отрицательное число. Прибавим к этой разности числа b и -b и сгруппируем слагаемые:

a - c = a - c + b - b = (а - b) + (b - с).

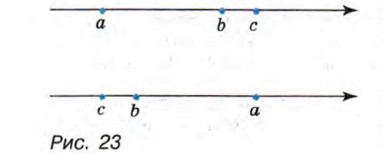
По условию а < b и b < с. Поэтому слагаемые а - b и b - с — отрицательные числа. Значит, и их сумма является отрицательным числом. Следовательно, а < с.

Аналогично доказывается, что если а > b и b > с, то а > с.

Геометрическая иллюстрация этих свойств дана на рисунке 23.

ТЕОРЕМА 3
Если а < b и с — любое число, то а + с < b + с.

Преобразуем разность (а + с) - (b + с):

(а + с) - (b + с) = а - b.

По условию а < b, поэтому а - b — отрицательное число. Значит, и разность (а + b) - (b + с) отрицательна. Следовательно, а + с < b + с.

Итак,

если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство.

ТЕОРЕМА 4
Если а < b и с — положительное число, то ас < bс. Если а < b и с — отрицательное число, то ас > bс.

АРХИМЕД

АРХИМЕД (287—212 гг. до н. э.) — древнегреческий математик, физик и механик. Разработал новые математические методы, в частности методы вычисления площадей криволинейных фигур и объёмов тел. Дал образцы применения математики к задачам естествознания и техники.

Представим разность ас - bс в виде произведения:

ас - bс = с (а - b).

Так как а < b, то а - b — отрицательное число. Если с > 0, то произведение с(а - b) отрицательно, и, следовательно, ас < bс. Если с < 0, то произведение с (а - b) положительно, и, следовательно, ас > bс.

Так как деление можно заменить умножением на число, обратное делителю, то аналогичное свойство справедливо и для деления. Итак,

если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство;
если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.

СЛЕДСТВИЕ
Если а и b — положительные числа и а < b, то

Продолжение >>>