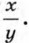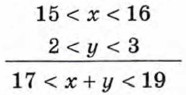Сложение и умножение числовых неравенств

Рассмотрим теперь, как выполняется сложение и умножение числовых неравенств.

ТЕОРЕМА 5
Если а < b и с < d, то а + с < b + d.

Прибавив к обеим частям неравенства а < b число с, получим а + с < b + с. Прибавив к обеим частям неравенства с < d число b, получим b + с < b + d. Из неравенств а + с < b + с и b + с < b + d следует, что а + с < b + d.

Теорема справедлива и в случае почленного сложения более чем двух неравенств.

Таким образом,

если почленно сложить верные неравенства одного знака, то получится верное неравенство.

ТЕОРЕМА б
Если а < b и с < d, где а, b, с и d — положительные числа, то ас < bd.

Умножив обе части неравенства а < b на положительное число с, получим ас < bс. Умножив обе части неравенства с < d на положительное число b, получим bc < bd. Из неравенств ас < bс и be < bd следует, что ас < bd.

Теорема справедлива и для почленного умножения более чем двух неравенств указанного вида.

Таким образом,

если почленно перемножить верные неравенства одного знака, левые и правые части которых — положительные числа, то получится верное неравенство.

Заметим, что если в неравенствах а < b и с < d среди чисел а, b, с и d имеются отрицательные, то неравенство ас < bd может оказаться неверным. Так, перемножив почленно верные неравенства -1 < 2 и -3 < 1, получим неравенство 3 < 2, которое не является верным.

СЛЕДСТВИЕ
Если числа а и b положительны и а < b, то аⁿ < bⁿ, где n — натуральное число.

Перемножив почленно п верных неравенств а < b, в которых а и b — положительные числа, получим верное неравенство аⁿ < bⁿ.

Доказанные свойства используются для оценки суммы, разности, произведения и частного.

Пусть, например, известно, что 15 < x < 16 и 2 < у < 3. Требуется оценить сумму х + у, разность х - у, произведение ху и частное

1. Оценим сумму х + у.

Применив теорему о почленном сложении неравенств к неравенствам 15 < х и 2 < у, а затем к неравенствам х < 16 и у < 3, получим 17 < х + у и х + y < 19. Результат можно записать в виде двойного неравенства 17 < х + у < 19. Запись обычно ведут короче:

Продолжение >>>