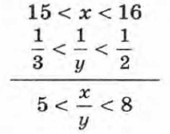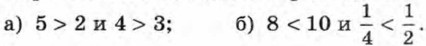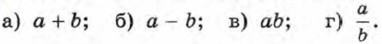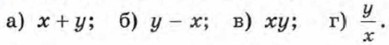|
|
|
|
|
§ 10. Числовые неравенства и их свойства Сложение и умножение числовых неравенств (продолжение)2. Оценим разность х - у. Для этого представим разность х - у в виде суммы х + (-у). Сначала оценим выражение -у. Так как 2 < у < 3, то -2 > -у > -3, т. е. -3 < -у < -2. Применим теперь теорему о почленном сложении неравенств:
3. Оценим произведение ху. Так как каждое из чисел х и у заключено между положительными числами, то они также являются положительными числами. Применив теорему о почленном умножении неравенств, получим
4. Оценим частное Для этого представим частное
Упражнения765. Сложите почленно неравенства: а) 12 > -5 и 9 > 7; б) -2,5 < -0,7 и -6,5 < -1,3. 766. Перемножьте почленно неравенства:
767. Верно ли для положительных чисел а и b, что: а) если а2 > b2, то а3 > b3; б) если а3 > b3, то а2 > b2? 768. Пусть 3 < a < 4 и 4 < b < 5. Оцените:
769. Зная, что 6 < x < 7 и 10 < у < 12, оцените:
770. Пользуясь тем, что 1,4 < √2 < 1,5 и 1,7 < √3 < 1,8, оцените: a) √2 + √3; б) √3 - √2. 771. Пользуясь тем, что 2,2 < √5 < 2,3 и 2,4 < √6 < 2 ,5, оцените: a) √6 + √5; б) √6 - √5. 772. Известны границы длин основания а и боковой стороны b равнобедренного треугольника, выраженные в миллиметрах: 26 ≤ а ≤ 28 и 41 ≤ b ≤ 43. Оцените периметр этого треугольника.
|
|
|



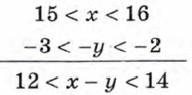
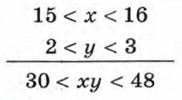
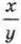 .
.
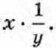 Сначала оценим выражение
Сначала оценим выражение 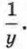 Так как 2 < у < 3, то
Так как 2 < у < 3, то 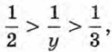 т. е.
т. е. 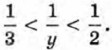 По теореме о почленном умножении неравенств имеем
По теореме о почленном умножении неравенств имеем