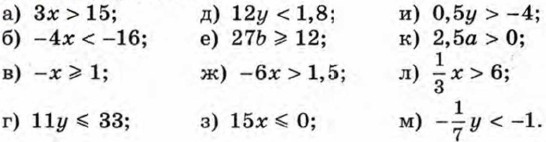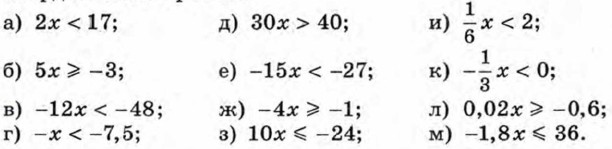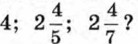|
|
|
|
|
§ 11. Неравенства с одной переменной и их системы Решение неравенств с одной переменной (продолжение)Пример 3. Решим неравенство
Отсюда -x < 12,
Ответ: (-12; +∞).
В приведённых примерах мы получали линейные неравенства, в которых коэффициент при переменной не равен нулю. Может случиться, что при решении неравенства мы придём к линейному неравенству вида 0 • х > b или 0 • х < b. Неравенство такого вида, а значит, и соответствующее исходное неравенство либо не имеют решений, либо их решением является любое число. Пример 4. Решим неравенство 2(х + 8) - 5х < 4 - 3х. Имеем 2х + 16 - 5х < 4 - 3х,
Приведём подобные члены в левой части неравенства и запишем результат в виде 0 • х: 0 • х < -12. Полученное неравенство не имеет решений, так как при любом значении х оно обращается в числовое неравенство 0 < -12, не являющееся верным. Значит, не имеет решений и равносильное ему заданное неравенство. Ответ: решений нет. Упражнения833. Является ли решением неравенства 5у > 2 (у - 1) + 6 значение у, равное: а) 8; б) -2; в) 1,5; г) 2? 834. Укажите два каких-либо решения неравенства 2х < х + 7. 835. Решите неравенство и изобразите множество его решений на координатной прямой:
836. Решите неравенство:
837. Решите неравенство и изобразите множество его решений координатной прямой:
837. Решите неравенство 5x +1 > 11. Укажите три каких-нибудь решения этого неравенства. 838. Решите неравенство 3х - 2 < 6. Является ли решением этого неравенства число: 840. Решите неравенство:
841. Решите неравенство и изобразите множество его решений на координатной прямой:
842. а) При каких значениях х двучлен 2х - 1 принимает положительные значения?
843. а) При каких значениях а значения двучлена 2а - 1 меньше значений двучлена 7 - 1,2а?
844. Решите неравенство:
845. Решите неравенство: а) 4(2 - 3x) - (5 - x) > 11 - х;
846. Решите неравенство и покажите на координатной прямой множество его решений:
847. Решите неравенство: а) 0,2x2 - 0,2(х - 6)(х + 6) > 3,6x;
|
|
|



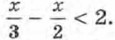
 Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство, т. е. на 6. Получим
Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство, т. е. на 6. Получим