|
|
|
|
|
§ 11. Неравенства с одной переменной и их системы Доказательство неравенств (окончание)Пример 4. Докажем, что при любом натуральном n > 1 верно неравенство
Складывая почленно эти неравенства и прибавляя к левой и правой частям полученного неравенства по
Отсюда
Неравенство доказано. Упражнения905. Докажите неравенство: а) а2 + b2 + 4 ≥ 2(а + b + 1); б) 4а2 + b2 > 4(а + b - 2). 906. Докажите, что если х > 0 и у > 0, то:
907. Докажите, что при а > 0 и b > 0 верно неравенство: а) (а + b)(аb + 16) ≥ 16аb;
908. Докажите, что:
909. Докажите, что куб полусуммы любых двух положительных чисел не превосходит полусуммы их кубов. 910. Докажите, что
если а > 0, b > 0, с > 0, d > 0. 911. Докажите, что при а > 0, b > 0, с > 0 верно неравенство
912. Докажите, что если х + у + z = 1, то
913. Докажите, что при любом а, большем 1, верно неравенство
914. Велосипедист рассчитал, с какой скоростью он должен ехать из посёлка в город и обратно, чтобы, пробыв в городе полчаса, вернуться в посёлок к намеченному сроку. Однако на пути из посёлка в город он ехал со скоростью, на 2 км/ч меньшей намеченной, а спустя полчаса возвращался из города в посёлок со скоростью, на 2 км/ч большей намеченной. Успел ли велосипедист вернуться в посёлок к назначенному сроку? Ответы907. Указание. Можно воспользоваться соотношением между средним арифметическим и средним геометрическим двух положительных чисел. 910. Указание. Сравните квадраты левой и правой частей неравенства. 912. Указание. Воспользуйтесь соотношениями вида 913. Указание. Можно воспользоваться тем, что 914. He успел.
|
|
|



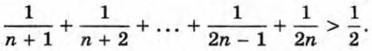
 Очевидно, что при любом натуральном n > 1 верны следующие неравенства:
Очевидно, что при любом натуральном n > 1 верны следующие неравенства:
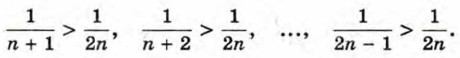
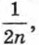 будем иметь
будем иметь
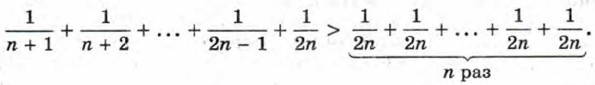
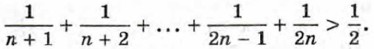

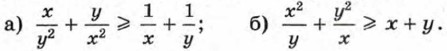
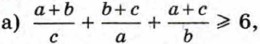 если а > 0, b > 0, с > 0;
если а > 0, b > 0, с > 0;
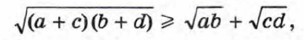
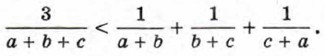
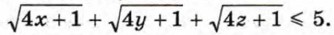
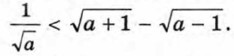
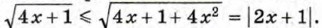
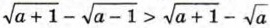 при a > 1.
при a > 1.