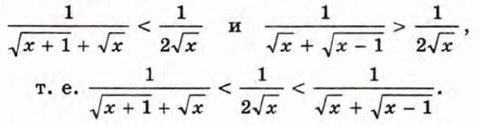|
|
|
|
|
§ 11. Неравенства с одной переменной и их системы Доказательство неравенствОдин из приёмов доказательства неравенств состоит в том, что составляют разность левой и правой частей неравенства и показывают, что она сохраняет знак при любых указанных значениях переменных. Этот приём вам уже приходилось применять в простых случаях. Покажем его применение на более сложном примере. Пример 1. Докажем, что
Для того чтобы оценить составленную разность, каждое из выражений, записанных в скобках, представим в виде дроби со знаменателем 1 и освободимся от иррациональности в её числителе. Получим
Так как функция у = √x является возрастающей, то знаменатель первой дроби меньше, чем знаменатель второй, т. е. первая дробь больше второй. Следовательно, разность дробей является положительной. Заданное неравенство доказано. Ещё один приём доказательства неравенств состоит в том, чтобы показать, что данное неравенство следует из других неравенств, справедливость которых известна. Пример 2. Докажем, что (a2 + bc)(b2 + ас)(с2 + ab) ≥ 8а2b2с2, если а > 0, b > 0, с > 0.
Перемножив эти неравенства, получим, что
Отсюда (а2 + bc)(b2 + ас) (с2 + ab) ≥ 8а2b2с2. Неравенство доказано. В отдельных случаях удаётся доказать неравенство, используя некоторые очевидные соотношения. В качестве таких очевидных соотношений могут быть взяты, например, такие: (1 + а)2 >1 + 2а при любом а, не равном нулю, Пример 3. Докажем, что двойное неравенство
верно при любом х ≥ 1.
Так как
Неравенство доказано.
|
|
|



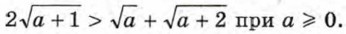
 Составим разность левой и правой частей неравенства и преобразуем её:
Составим разность левой и правой частей неравенства и преобразуем её:
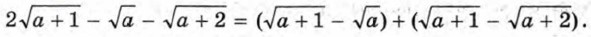
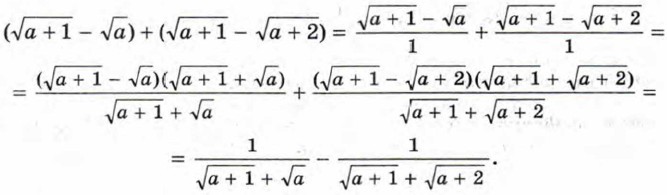

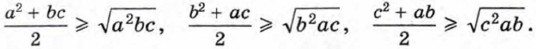
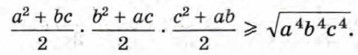
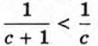 при с > 0,
при с > 0, 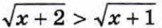 при х ≥ -1 и т. п.
при х ≥ -1 и т. п.
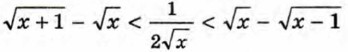
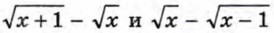 соответственно равными им дробями
соответственно равными им дробями 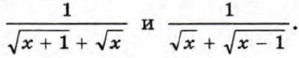 Тогда данное неравенство примет вид
Тогда данное неравенство примет вид
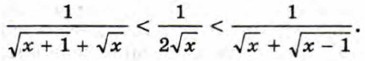
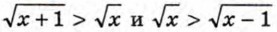 при x ≥ 1, то
при x ≥ 1, то