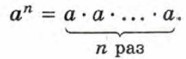Выражения и их преобразования

1. Степенью числа а с натуральным показателем n, бо́льшим 1, называют произведение n множителей, каждый из которых равен а:

Степенью числа а с показателем 1 называют само число а:

a¹ = a

Степень числа а ≠ 0 с показателем 0 равна 1:

a⁰ = 1

2. Свойства степеней с натуральными показателями:

а) а^m • аⁿ = а^{m + n}.

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

б) а^m : аⁿ - а^{m - n}, где а ≠ 0, m ≥ n.

При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

в) (а^m)ⁿ = а^mn.

При возведении степени в степень основание оставляют прежним, а показатели перемножают.

г) (ab)ⁿ = аⁿbⁿ.

При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.

3. Одночленами называют произведения чисел, переменных и их степеней, а также сами числа, переменные и их степени. Например, 5а²х, -3а²b³, 4, х, у⁵ — одночлены.

Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена -8а²b⁴ равна 6.

4. Многочленом называют сумму одночленов. Например, 3x⁵ - 4х² + 1, 7а³b - ab² + аb + 6 — многочлены. Одночлены считают многочленами, состоящими из одного члена.

Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х³у + 3х²у⁵ + ху равна степени одночлена 3х²у⁵, т. е. равна 7.

Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.

5. При сложении многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,

(3аb + 5с²) + (ab - с²) = 3ab + 5с² + ab - с² = 4аb + 4с².

При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,

(6х² - у) - (2х² - 8у) = 6х² - у - 2х² + 8у = 4х² + 7у.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,

a²(3ab - b³ + 1) = 3а³b - а²b³ + а².

Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,

(5х - 1)(3х + 2) = 15х² - 3х + 10х - 2 = 15х² + 7х - 2.

Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.

Окончание >>>