Функция 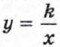и её график (продолжение)

Упражнения

179. Функция задана формулой 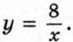Заполните таблицу.

180. Обратная пропорциональность задана формулой 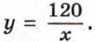Заполните таблицу.

181. Двигаясь со скоростью υ км/ч, поезд проходит расстояние между городами А и В, равное 600 км, за t ч. Запишите формулу, выражающую зависимость: a) υ от t; б) t от υ.

182. Обратная пропорциональность задана формулой 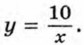Найдите значение функции, соответствующее значению аргумента, равному 100; 1000; 0,1; 0,02. Определите, принадлежит ли графику этой функции точка А (-0,05; -200), В (-0,1; 100), С (400; 0,025), D (500; -0,02).

183. Известно, что некоторая функция — обратная пропорциональность. Задайте её формулой, зная, что значению аргумента, равному 2, соответствует значение функции, равное 12.

184. На рисунке 6 построен график функции, заданной формулой 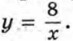Найдите по графику:

а) значение у, соответствующее значению х, равному 2; 4; —1; -4; -5;
б) значение х, которому соответствует значение у, равное -4; —2; 8.

185. Постройте график функции, заданной формулой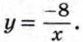

а) значение у, соответствующее значению х, равному 4; 2,5; 1,5; —1; -2,5;
б) значение х, которому соответствует значение у, равное 8; -2.

186. Постройте график функции 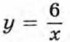и, используя его, решите уравнение:

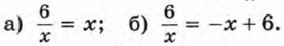
187. Решите графически уравнение: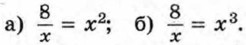

188. (Для работы в парах.) Используя графические представления, выясните, сколько решений имеет уравнение:

1) Распределите, кто выполняет задания а) и г), а кто — задания б) и в), и выполните их.
2) Проверьте друг у друга, верно ли построены графики функции .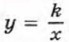
3) Обсудите правильность сделанных выводов о числе решений уравнения.

189. Прямоугольный параллелепипед со сторонами основания а см и b см и высотой 20 см имеет объём, равный 120 см³. Выразите формулой зависимость b от а. Является ли эта зависимость обратной пропорциональностью? Какова область определения этой функции? Постройте график.

<<< К началу Окончание >>>