|
|
|
|
|
§ 3. Произведение и частное дробей Представление дроби в виде суммы дробейСумму двух рациональных дробей, как известно, всегда можно представить в виде несократимой дроби, у которой числитель и знаменатель — многочлены с переменными или числа (в частности, число 1). Обратная задача — представление дроби в виде суммы двух дробей — неопределённая. Так, например, дробь
Вообще задача представления дроби в виде суммы дробей допускает сколь угодно много решений. Действительно, если требуется представить дробь Для представления дроби в виде суммы дробей можно воспользоваться методом неопределённых коэффициентов. Разъясним на примере, в чём состоит этот метод. Пример 1. Представим дробь
Сложим дроби в правой части равенства:
Получаем, что Это равенство будет тождеством, если а + b = 7 и 4а - 3b = 0. Решив систему уравнений
найдём, что а = 3, b = 4. Следовательно,
Приведём теперь примеры задач, при решении которых используется представление дроби в виде суммы целого выражения и дроби. Пример 2. Найдём все пары целых чисел, удовлетворяющие уравнению х - ху + 3у = 5.
Выделив из дроби
Значение дроби Пример 3. Найдём, при каких значениях n значение дроби
В результате получаем, что частное равно n + 3, а остаток равен 5. Значит, n2 - 2n - 10 = (n - 5) (n + 3) + 5. Отсюда
Значение двучлена n + 3 при любом целом л является целым числом. Значение дроби Значит, дробь
|
|
|



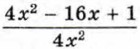 можно представить в виде суммы (или разности) двух слагаемых разными способами:
можно представить в виде суммы (или разности) двух слагаемых разными способами:
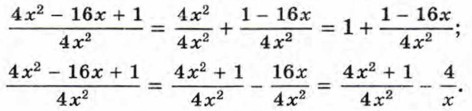
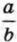 в виде суммы двух дробей, то в качестве одного из слагаемых можно взять произвольную дробь
в виде суммы двух дробей, то в качестве одного из слагаемых можно взять произвольную дробь 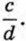 Тогда вторая дробь будет равна разности
Тогда вторая дробь будет равна разности 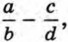 т. е. равна дроби
т. е. равна дроби 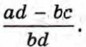
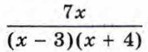 в виде суммы дробей со знаменателями х - 3 и х + 4.
в виде суммы дробей со знаменателями х - 3 и х + 4.
 Допустим, что
Допустим, что
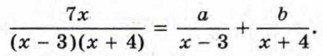
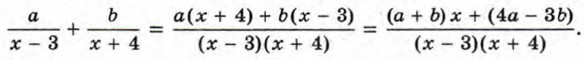
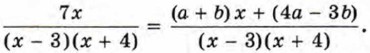
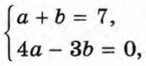
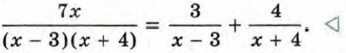
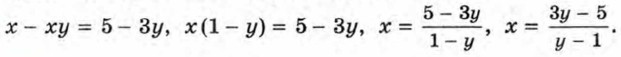
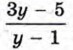 целую часть, получим
целую часть, получим
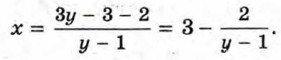
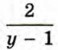 является целым числом тогда и только тогда, когда у - 1 = -2, у - 1 = -1, у - 1 = 1, у - 1 = 2. Отсюда у = -1; 0; 2; 3. Вычисляя соответствующее значение х, получаем искомые пары целых чисел: (4; -1), (5; 0), (1; 2), (2; 3).
является целым числом тогда и только тогда, когда у - 1 = -2, у - 1 = -1, у - 1 = 1, у - 1 = 2. Отсюда у = -1; 0; 2; 3. Вычисляя соответствующее значение х, получаем искомые пары целых чисел: (4; -1), (5; 0), (1; 2), (2; 3). 
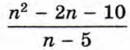 является целым числом.
является целым числом.
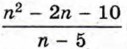 в виде суммы многочлена и дроби. Для этого многочлен n2 - 2n - 10 разделим на двучлен n - 5. Деление выполним уголком аналогично тому, как выполняется деление натуральных чисел.
в виде суммы многочлена и дроби. Для этого многочлен n2 - 2n - 10 разделим на двучлен n - 5. Деление выполним уголком аналогично тому, как выполняется деление натуральных чисел.
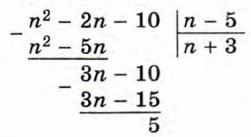
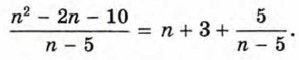
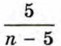 является целым числом тогда и только тогда, когда n - 5 равно 1, -1, 5 или -5.
является целым числом тогда и только тогда, когда n - 5 равно 1, -1, 5 или -5.
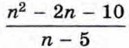 принимает целые значения при n, равном 0, 4, 6 и 10.
принимает целые значения при n, равном 0, 4, 6 и 10.