|
|
|
|
|
Для тех, кто хочет знать больше Дробно-линейная функция и ее график (продолжение)Для построения графика данной функции поступим так: про ведем в координатной плоскости пунктиром асимптоты: прямую х = 1 и прямую у = 2. Так как гипербола состоит из двух ветвей, то для построения этих ветвей составим две таблицы: одну для х < 1, другую для х > 1.
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы. График функции Пример 2. Построим график функции
В этом случае k = 3, m = -1, n = -2. График функции Далее поступим так. Проведем в координатной плоскости пунктиром асимптоты y = -2 и x = -1. Составим две таблицы: одну для х < -1, другую для x > -1.
Отметив в координатной плоскости точки, координаты которых помещены в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Используя вторую таблицу, получим вторую ветвь гиперболы. График функции
В примерах 1 и 2 мы установили, что графиком каждой из функции Можно доказать, что любую дробно-линейную функцию Таким образом, графиком дробно-линейной функции является гипербола, которую можно получить из гиперболы
|
|
|




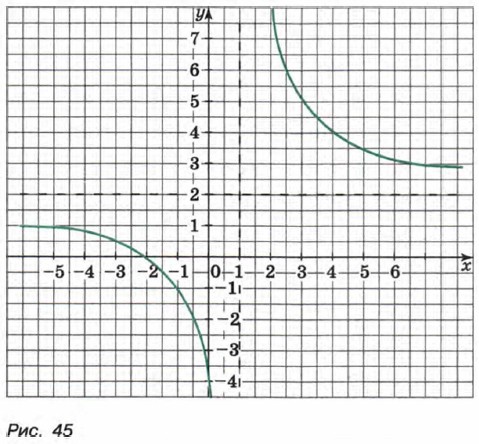
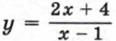 изображен на рисунке 45.
изображен на рисунке 45. 
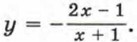
 Так же как и в примере 1, выделим из дроби
Так же как и в примере 1, выделим из дроби 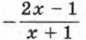 целую часть, т. е. представим дробь в виде
целую часть, т. е. представим дробь в виде 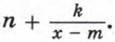 Имеем
Имеем
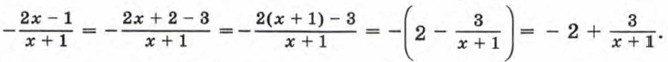
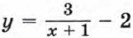 можно получить из графика функции
можно получить из графика функции 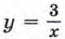 помощью двух параллельных переносов: сдвига гиперболы
помощью двух параллельных переносов: сдвига гиперболы 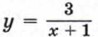 на 2 единицы вниз. При этом асимптотами гиперболы
на 2 единицы вниз. При этом асимптотами гиперболы 
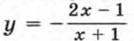 изображен на рисунке 46.
изображен на рисунке 46. 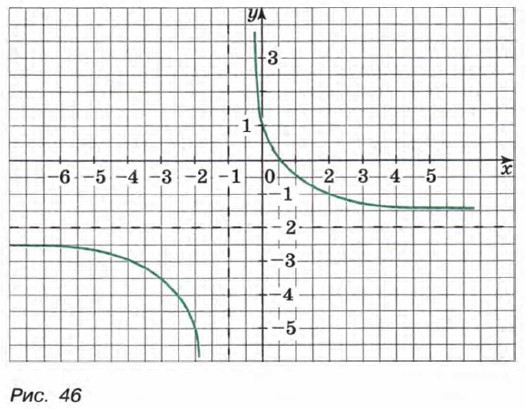
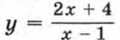 и
и 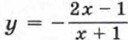 является гипербола, и показали один из способов построения графиков этих функций.
является гипербола, и показали один из способов построения графиков этих функций.
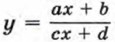 можно представить в виде
можно представить в виде 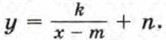
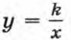 с помощью двух параллельных переносов.
с помощью двух параллельных переносов.