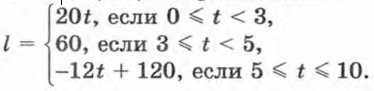|
|
|
|
|
Дополнительные упражнения к главе I К параграфу 1200. Найдите область определения функции:
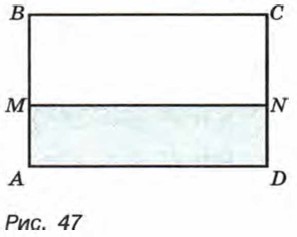
201. Длина прямоугольника ABCD (рис. 47) равна 10 см, а ширина — 7 см. Отрезок MN передвигается от отрезка AD до отрезка ВС, оставаясь параллельным отрезку AD. Площадь у (см2) закрашенной части есть функция расстояния х (см) от точки D до точки N. Задайте функцию у = ƒ(x) формулой. Найдите область значений этой функции. 202. В равнобедренном треугольнике АВС основание АС равно 6 см, а боковая сторона — 5 см. Концы подвижного отрезка, параллельного основанию, лежат на боковых сторонах. Его длина равна у (см), а расстояние от вершины — х (см). Задайте формулой у как функцию от х. Найдите область значений этой функции. 203. Функция задана формулой 204. Катер отправляется от пристани А и идет вниз по реке к пристани В, до которой 60 км. После двухчасовой стоянки на пристани В он возвращается обратно. Расстояние l (км), пройденное катером от пристани А, зависит от времени t (ч), отсчитываемого с момента отправления катера из А до момента возвращения. Собственная скорость катера 16 км/ч, скорость течения реки 4 км/ч. Задайте l как функцию от t формулами, постройте график функции, опишите по графику ее свойства и объясните их физический смысл. 205. Начертите график какой-нибудь функции, областью определения которой является промежуток [-3; 4], а областью значений — промежуток [0; б]. 206. Найдите нули функции (если они существуют):
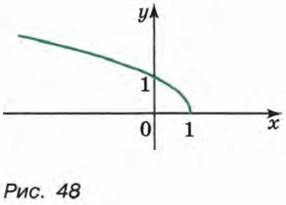
207. Известно, что у = ƒ(x) и у = g(x) — возрастающие (убывающие) функции. Докажите, что функция φ(x) = ƒ(x) + g(x) является возрастающей (убывающей) функцией. 208. Известно, что у = ƒ(x) — возрастающая функция и a — некоторое число. Докажите, что уравнение ƒ(x) = а имеет не более одного корня. 209. Решите уравнение: а) √х + х2 = 18; б) х3 + 5х = 6. 210. Какие из функций, заданных формулами у = х2, у = х2 + 5, У = 2х + 5, у = х3, у = -х2, у = -х2 - 4, у = √x, у = √x + 1, у = х4 + х2 + 6, сохраняют знак на всей области определения? 211. На рисунке 48 изображен график Рис. 48 одной из функций
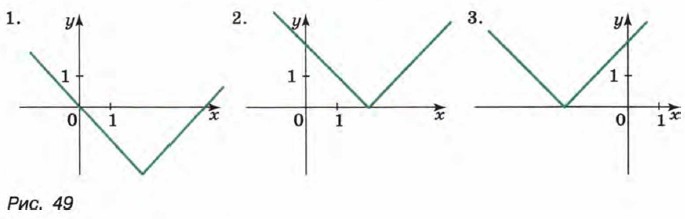
212. Какой из трех графиков, изображенных на рисунке 49, является графиком функции у = |х - 2|?
213. Постройте график функции Ответы200. а) (-∞; -6) ∪ (-6; 0) ∪ (0; +∞); б) [4; +∞); в) (-∞; -1) и (-1; 0) U (0; +∞). 201. у = 10х, где 0 ≤ х ≤ 7; [0; 70]. 202. у = 1,5х, где 0 ≤ х ≤ 4; [0; 6]. 203. График не пересекает ось х, а ось у пересекает в точке (0; 1). Он расположен в I и II координатных четвертях. 204. 209. а) 4; б) 1. 210. у = х2 + 5, у = -x2 - 4, y = √x + 1, y = x4 + x2 + 6
|
|
|



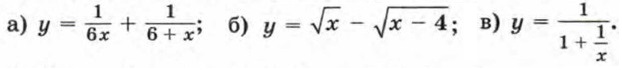
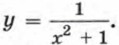 Пересекает ли ее график ось x? ось у? В каких координатных четвертях расположен график этой функции?
Пересекает ли ее график ось x? ось у? В каких координатных четвертях расположен график этой функции?
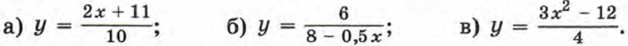
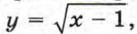
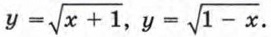
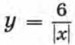 и опишите ее свойства.
и опишите ее свойства.