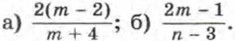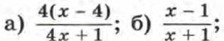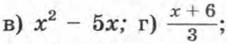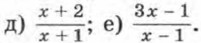|
|
|
|
|
Дополнительные упражнения к главе I К параграфу 2214. Найдите корни квадратного трехчлена:
215. Составьте какой-нибудь квадратный трехчлен, корнями которого являются числа: а) -7 и 2; б) 3 - √2 и 3 + √2. 216. При каком значении р выражение 2рх2 - 2х - 2р - 3 становится квадратным трехчленом, одним из корней которого является число нуль? Найдите другой корень. 217. Докажите, что квадратный трехчлен имеет корни, и найдите их сумму и произведение:
218. Найдите трехчлен вида х2 + рх + q, корнями которого являются не равные нулю числа р и q. 219. Пусть α и β — корни трехчлена х2 + рх + q, причем αβ = 4 и √α + √β = 3. Чему равны α и β? 220. Выделите квадрат двучлена из квадратного трехчлена:
221. Докажите, что квадратный трехчлен: а) -x2 + 20л; - 103 не принимает положительных значений;
222. Найдите наибольшее или наименьшее значение квадратного трехчлена: а) 3x2 - 4x + 5; б) -3x2 + 12x. 223. Сумма положительных чисел а и b равна 40. При каких значениях а и b их произведение будет наибольшим? 224. Разложите на множители квадратный трехчлен:
225. Зная, что m — целое число, найдите целые корни трехчлена mх2 + (m - 3)x - 3. 226. Зная, что коэффициенты квадратного трехчлена (n - 3)х2 + (n + 1)х + 9 - 2n — натуральные числа, найдите этот трехчлен. 227. Сократите дробь:
228. Выполните действие:
Ответы214. а) -6; 2; 216. При р = -1,5; 218. х2 + х - 2. 219. α = 1, β = 4 или α = 4, β = 1. 222. а) 223. При а = b = 20. 225. -1 и 1, или -1 и 3, или -1 и -3, или -1 и -1. 226. х2 + 5х + 1. 227. 228.
|
|
|



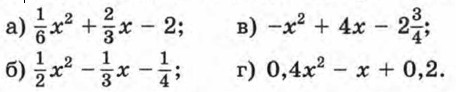

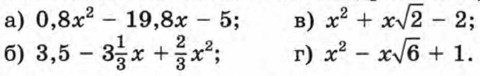
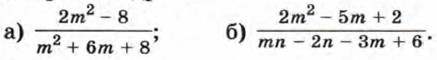
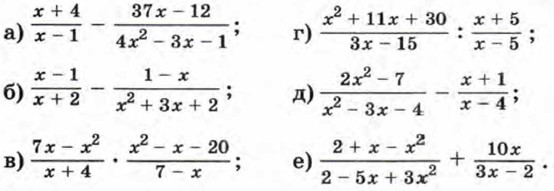
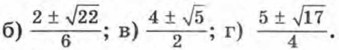
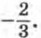
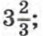 б) 12.
б) 12.