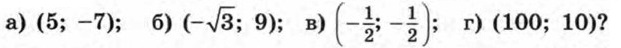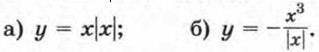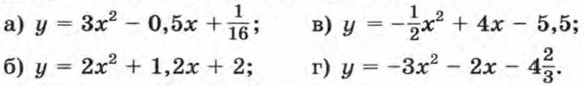К параграфу 3

229. При каком значении а график функции у = ах² проходит через точку:

230. Постройте график функции, заданной формулой у = -0,25х², где х ∈ [-6; 2]. Каковы наибольшее и наименьшее значения этой функции?

231. При каких значениях а областью значений функции у = ах² является промежуток: а) [0; +∞); б) (-∞; 0]?

232. Докажите, что графики функций у = ах² и у = ах, где а ≠ 0, пересекаются в точке (1; а). В какой еще точке пересекаются эти графики?

233. Параболу у = 7х² сдвинули вверх на 5 единиц и влево на 8 единиц. Графиком какой функции является полученная парабола?

234. Какие преобразования надо выполнить, чтобы:

а) из графика функции у = х³ получить графики функций
у = -х³, у = (х - 3)³, у = х3 + 4;
б) из графика функции у = √х получить графики функций
у = -√х, у = √х + 5, у = √х - 1?

235. Постройте в одной координатной плоскости графики функций:

у = |х|, у = |х - 4|, у = |х - 4| - 3.

236. Постройте график функции:

a) ƒ(x) = |х² - 2х|, б) ƒ(x) = х² - 2|х|.

237. Постройте график функции:

238. При каких значениях с график функции у = х² - 6х + с расположен выше прямой:

а) у = 4; б) у = -1?

239. При каких значениях Ь и с вершиной параболы у = х² + bх + с является точка (6; -12)?

240. Найдите значение а, при котором осью симметрии параболы у = ах² - 16х + 1 является прямая х = 4.

241. При каких значениях а и с квадратичная функция у = ах² + с имеет нули?

242. Найдите значения а и b, при которых график функции у = ах² + bх - 18 проходит через точки М(1; 2) и N(2; 10).

243. Постройте график функции и опишите ее свойства:

а) у = х² + 2х - 15;
б) у = 0,5х² - 3х + 4;
в) у = 4 - 0,5x²;

г) у = 6х - 2х²;
д) у = (2x - 7)(х + 1);
е) у = (2 - х)(х + 6).

244. Найдите область значений функции:

245. Пусть h (м) — высота, на которой находится брошенный с земли вверх мяч, t (с) — время полета мяча. Зависимость h от t выражается формулой h = 24t - 4,9t². Какой наибольшей высоты достиг мяч? В какой промежуток времени он поднимался и в какой опускался? Через сколько секунд после броска он упал на землю?

246. Задайте формулой какую-либо квадратичную функцию, которая:

а) в промежутке (-∞; -3] убывает, а в промежутке [-3; +∞) возрастает;
б) в промежутке (-∞; 6] возрастает, а в промежутке [6; +∞) убывает.

247. Функция задана формулой у = х² + рх + q. Найдите значения р и q, если известно, что:

а) нули функции — числа 3 и 4;
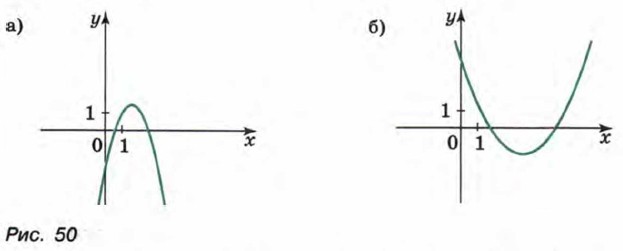
б) график функции пересекает оси координат в точках (0; 6) и (2; 0);
в) наименьшее значение, равное 24, функция принимает при х = 6.

248. По графику функции у = ах² + bх + с (рис. 50, а, б) определите знаки коэффициентов а, b и с.

Ответы

229. а) При а = -0,28; б) при а = 3; в) при а = -2; г) при а = 0,001.

238. а) При с > 13; б) при с > 8.

239. При b = -12, с = 24.

240. При а = 2.

241. При а > 0 и с ≤ 0; при а < 0 и с ≥ 0.

242. При а = -6 и b = 26.