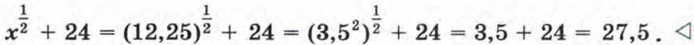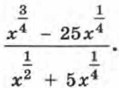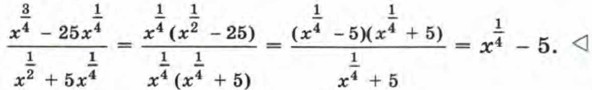|
|
|
|
|
Для тех, кто хочет знать больше Степень с рациональным показателемВ п.9 говорилось, что выражение
По определению имеем:
Степень с основанием, равным нулю, определяется только для положительного дробного показателя:
Для отрицательных оснований степень с дробным показателем не рассматривается. Такие выражения, как Известные нам свойства степени с целым показателем справедливы и для степени с любым рациональным показателем. С их доказательством вы ознакомитесь в старших классах. Перечислим эти свойства.
Рассмотрим примеры, в которых используются тождественные преобразования выражений, содержащих степени с дробными показателями. Пример 1. Найдем значение выражения
Подставим в выражение
Пример 2. Сократим дробь
|
|
|



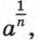 где а > 0 и n — натуральное число, обозначает
где а > 0 и n — натуральное число, обозначает 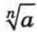 . Теперь рассмотрим какой смысл имеет выражение
. Теперь рассмотрим какой смысл имеет выражение 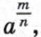 где а — положительное число,
где а — положительное число, 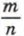 — дробное число.
— дробное число.
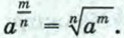
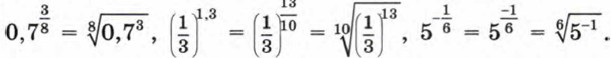
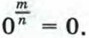
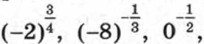 не имеют смысла.
не имеют смысла.
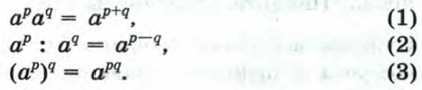

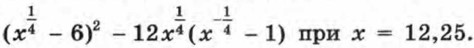
 Предварительно упростим это выражение:
Предварительно упростим это выражение:
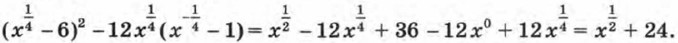
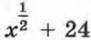 данное значение х и выполним вычисления:
данное значение х и выполним вычисления: