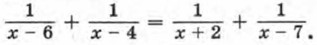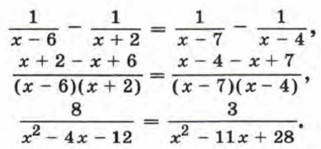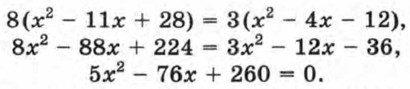|
|
|
|
|
§ 5. Уравнения с одной переменной Дробные рациональные уравненияВ каждом из уравнений
левая и правая части представляют собой рациональные выражения, причем либо оба выражения являются дробными, либо одно из них является дробным, а другое — целым выражением. Такие уравнения, как вы знаете, называются дробными рациональными уравнениями. Напомним, что
При решении дробных рациональных уравнений, как вам известно, обычно поступают следующим образом: С простейшими примерами решения дробных рациональных уравнений вы уже встречались. Рассмотрим более сложные примеры. Пример 1. Решим уравнение
6x2 - 54 + 9х = х3. Отсюда х3 - 6х2 - 9х + 54 = 0. (2) Решим полученное целое уравнение, используя разложение левой части на множители. Имеем (х3 - 6x2) - (9х - 54) = 0,
Значит, уравнение (2) имеет три корня: x1 = 6, х2 = 3, х3 = -3. Теперь необходимо проверить, не обращают ли найденные корни в нуль общий знаменатель дробей, входящих в уравнение (1). Если х = 6, то х4 - х2 - 72 ≠ 0;
Значит, уравнение (1) имеет единственный корень — число 6. Ответ: 6. Пример 2. Решим уравнение
Получим
Отсюда
Решив это уравнение, найдем, что оно имеет два корня: х1 = 5,2 и х2 = 10. Каждое из этих чисел не обращает в нуль знаменатели дробей, входящих в исходное уравнение. Следовательно, исходное уравнение имеет два корня: 5,2 и 10. Ответ: 5,2 и 10.
|
|
|



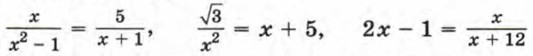
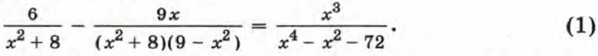
 Общий знаменатель дробей, входящих в уравнение, равен x4 - x2 - 72. Умножив обе части уравнения на общий знаменатель дробей, получим
Общий знаменатель дробей, входящих в уравнение, равен x4 - x2 - 72. Умножив обе части уравнения на общий знаменатель дробей, получим