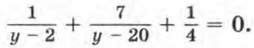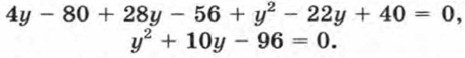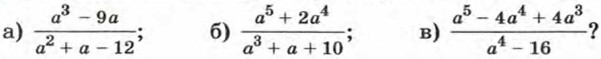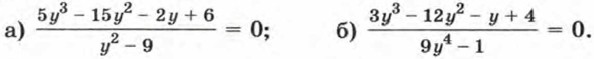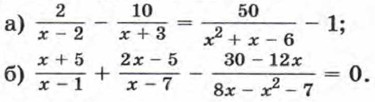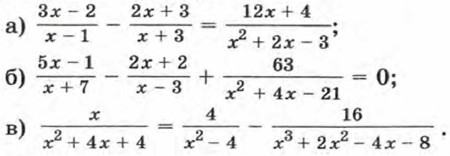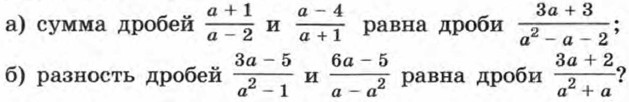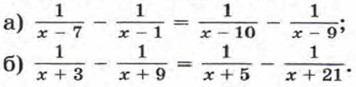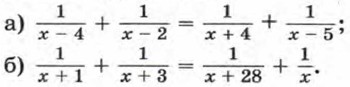Дробные рациональные уравнения (продолжение)

Пример 3. Решим уравнение

Умножив обе части уравнения на х - 2, получим целое уравнение

2х² - 3х - 2 = х²(х - 2). (4)

Разложив на множители квадратный трехчлен 2х² - 3х - 2, представим это уравнение в виде

(х - 2)(2х + 1) = х²(х - 2).

Отсюда

х²(х - 2) - (х - 2)(2х + 1) = 0,
(х - 2)(х² - 2х - 1) = 0,
х - 2 = 0 или х² - 2х - 1 = 0.

Решив полученные уравнения, найдем, что уравнение (4) имеет три корня: 2, 1 - √2, 1 + √2.

Остается проверить, не обращают ли они в нуль знаменатель х - 2. Если х = 2, то х - 2 = 0; если х = 1 - √2, то х - 2 ≠ 0; если х = 1 + √2, то х - 2 ≠ 0.

Значит, число 2 не является корнем уравнения (3), а числа 1 - √2 и 1 + √2 являются его корнями.

Ответ: 1 - √2 и 1 + √2.

В отдельных случаях удается решить дробное рациональное уравнение, используя введение новой переменной.

Пример 4. Решим уравнение

Введем новую переменную у = х² + х. Получим

Отсюда

Решив полученное квадратное уравнение, найдем, что

у = 6 или у = - 16.

Уравнение х² + х = 6 имеет два корня: -3 и 2. Уравнение х² + х = -16 корней не имеет.

Каждое из чисел -3 и 2 не обращает в нуль знаменатели дробей исходного уравнения и, следовательно, является его корнем.

Ответ: -3, 2.

Упражнения

288. При каких значениях а равно нулю значение дроби:

289. Решите уравнение:

290. Решите уравнение:

291. Найдите корни уравнения:

292. При каких значениях а:

293. Найдите корни уравнения:

294. Решите уравнение:

<<< К началу Окончание >>>