|
|
|
|
|
§ 6. Неравенства с одной переменной Решение неравенств методом интервалов (продолжение)Пример 2. Решим неравенство x(0,5 — х)(х + 4) < 0.
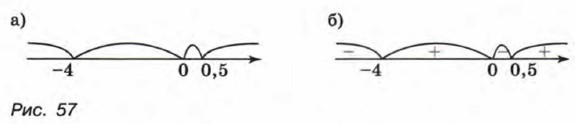
-х(х - 0,5 )(л; + 4) < 0, отсюда х(х - 0,5)(x + 4) > 0. Мы получили неравенство вида (1), равносильное данному. Отметим на координатной прямой нули функции ƒ(x) = х(х - 0,5)(x + 4)
(рис. 57, а). Покажем знаком «плюс», что в крайнем справа промежутке функция принимает положительное значение, а затем, двигаясь справа налево, укажем знак функции в каждом из промежутков (рис. 57, б). Получим, что множеством решений неравенства является объединение промежутков (-4; 0) и (0,5; +∞). Ответ: (-4; 0) ∪ (0,5; +∞). Пример 3. Решим неравенство (5х + 1)(5 - х) ≥ 0.
Разделив обе части неравенства на -5, будем иметь
Отметим на координатной прямой нули функции
т. е. точки
Заметим, что данное неравенство можно решить иначе, используя свойства графика квадратичной функции. Пример 4. Решим неравенство
(7 - х)(х + 2) < 0. Приведя неравенство (7 - х)(х + 2) < 0 к виду (1) и используя метод интервалов, найдем, что множеством решений этого неравенства, а значит, и исходного неравенства Ответ: (-∞; -2) ∪ (7; +∞).
|
|
|



 Приведем данное неравенство к виду (1). Для этого в двучлене 0,5 - х вынесем за скобку множитель -1. Получим
Приведем данное неравенство к виду (1). Для этого в двучлене 0,5 - х вынесем за скобку множитель -1. Получим

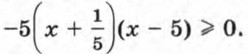
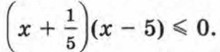
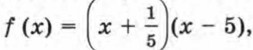
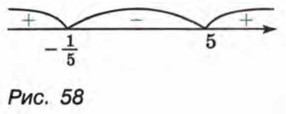
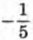 и 5, и укажем знаки функции в образовавшихся промежутках (рис. 58). Мы видим, что множество решений неравенства состоит из чисел
и 5, и укажем знаки функции в образовавшихся промежутках (рис. 58). Мы видим, что множество решений неравенства состоит из чисел 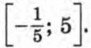
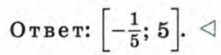
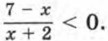
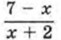 имеет смысл, ее знак совпадает со знаком произведения (7 - х)(х + 2), то данное неравенство равносильно неравенству
имеет смысл, ее знак совпадает со знаком произведения (7 - х)(х + 2), то данное неравенство равносильно неравенству