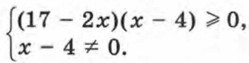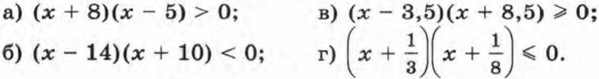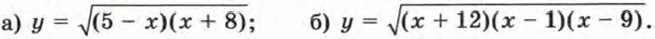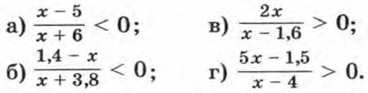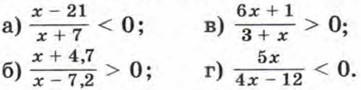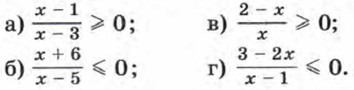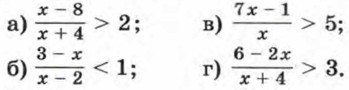|
|
|
|
|
§ 6. Неравенства с одной переменной Решение неравенств методом интервалов (окончание)Пример 5. Решим неравенство
Неравенство (17 - 2х)(х - 4) ≥ 0 приведем к виду (х - 8,5)(х - 4) ≤ 0. Решив это неравенство методом интервалов и исключив из множества его решений число 4, найдем, что множеством решений исходного неравенства является промежуток (4; 8,5]. Ответ: (4; 8,5]. Упражнения325. Решите неравенство, используя метод интервалов:
326. Решите неравенство:
327. Решите неравенство: а) (х - 2)(х - 5)(х - 12) > 0;
328. Найдите, при каких значениях х: а) произведение (х + 48)(х - 37)(х - 42) положительно;
329. Решите неравенство: а) (х + 9)(х - 2)(х - 15) < 0;
330. Найдите множество решений неравенства:
331. Решите неравенство: а) 2(х - 18)(х - 19) > 0;
332. Найдите область определения функции:
333. При каких значениях х имеет смысл выражение:
334. Решите неравенство:
335. Решите неравенство:
336. Найдите множество решений неравенства:
337. Решите неравенство:
338. Решите неравенство:
|
|
|



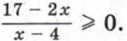
 Знак дроби
Знак дроби 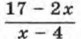 совпадает со знаком произведения (17 - 2х)(х - 4) при всех значениях х, при которых дробь имеет смысл. Поэтому данное неравенство равносильно системе
совпадает со знаком произведения (17 - 2х)(х - 4) при всех значениях х, при которых дробь имеет смысл. Поэтому данное неравенство равносильно системе