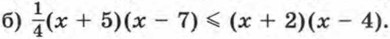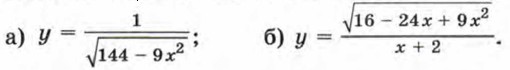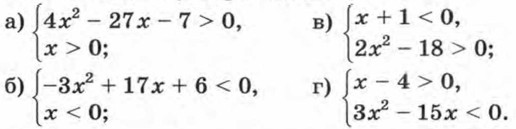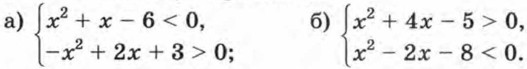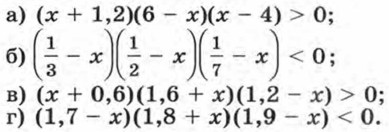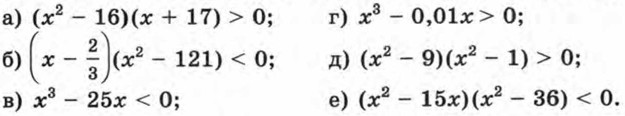|
|
|
|
|
Дополнительные упражнения К параграфу 6376. Решите неравенство:
377. Докажите, что при любом значении х верно неравенство: а) 2(х + 1)(x - 3) > (х + 5)(х - 7);
378. Найдите область определения функции:
379. При каких значениях а уравнение (а + 2)x2 + 8х + а — 4 = 0 имеет два корня? 380. При каких значениях b уравнение (6 - 1)х2 + 6х + b - 3 = 0 не имеет корней? 381. При каких значениях с не имеет корней уравнение: а) х4 - 12х2 + с = 0; б) х4 + сх2 + 100 = 0? 382. При каких значениях k уравнение х4 - 13x2 + k = 0 имеет: а) четыре корня; б) два корня? 383. Найдите общие решения неравенств х2 + 6х - 7 < 0 и х2 - 2х - 15 < 0. 384. Решите систему неравенств:
385. Решите систему неравенств:
386. Решите неравенство:
387. При каких значениях х произведение (3а: - 5) (x + 4) (2 - х): а) равно нулю; б) положительно; в) отрицательно? 388. Решите неравенство:
389. Решите неравенство, разложив его левую часть на множители:
|
|
|